
Să zicem că te afli într-un concurs televizat și ți se oferă posibilitatea alegerii dintre trei uși. În spatele unei uși se află un automobil; în spatele celorlalte două uşi se află capre. Desigur, îţi doreşti să câştigi maşina. Alegi o ușă, să zicem uşa nr. 1. Gazda concursului, care știe ce se află în spatele ușilor, nu te lasă să vezi ce este în spatele uşii pe care ai ales-o şi deschide încă o ușă, să zicem uşa nr. 3, în spatele căreia vezi că este o capră. Apoi gazda îţi oferă şansa să-ţi schimbi opţiunea, dar, desigur, fără a te uita la ce e în spatele uşii pe care ai ales-o, ştiind deja că în spatele uşii nr. 3 este o capră.
Întrebarea pentru tine e următoarea: este în avantajul tău să-ţi schimbi opţiunea? Cresc şansele de a câştiga maşina dacă alegi uşa nr. 2?
Gândeşte-te un pic, decide-te dacă este util să-ţi schimbi opţiunea, apoi citeşte restul articolului.
Probabil că prima ta reacţie este să spui că nu contează dacă îţi schimbi sau nu opţiunea. La urma urmelor, înainte să alegi exista o probabilitate de 33% de a găsi maşina, iar acum, după deschiderea unei uşi, probabilitatea de a găsi maşina în spatele oricărei uşi rămase este de 50%.
Această întrebare i-a fost adresată în anul 1990 de un cititor lui Marilyn vos Savant, aceasta fiind responsabilă pentru rubrica "Ask Marilyn" din revista Parade, SUA.
Răspunsul dat de vos Savant, care figura în Cartea Recordurilor ca femeia cu cel mai înalt coeficient de inteligenţă (IQ) din lume, a fost acela că trebuie schimbată opţiunea (trebuie aleasă uşa nr. 2) pentru a creşte probabilitatea de a câştiga maşina.
Concurenții care schimbă uşa au două din trei (2/3) șanse de a câștiga maşina, în timp ce concurenții care rămân la alegerea inițială au doar una din trei (1/3) șanse.
Mulți cititori au refuzat să creadă că schimbarea opțiunii inițiale este utilă, aproximativ 10.000 de persoane, dintre care aproape 1.000 cu doctorat, au scris revistei, majoritatea susținând că vos Savant se înșală. Mulţi au numit-o "idioată" şi au acuzat-o că păcăleşte publicul cu explicaţiile ei. Matematicianul Paul Erdős însuşi, unul dintre cei mai prolifici autori de lucrări în istoria matematicii, a fost greu de convins. În acest articol (eng.) poţi citi amintirile lui Andrew Vazsonyi cu privire la cum (nu) l-a convins pe matematician despre justeţea soluţiei lui Marlyn.
· Explicaţia vizuală a problemei lui Monty Hall
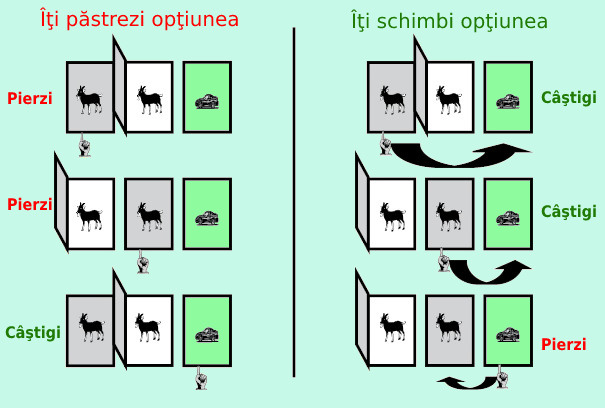
· Explicaţia pas cu pas
Din imagine rezultă clar că schimbarea opţiunii ajută, schimbând probabilitatea de a câştiga maşina. Dar de ce funcţionează?
Când gazda emisiunii deschide uşa, aceasta îţi dă mai multă informaţie despre ce se află în spatele uşilor.
Gazda ştie în spatele cărei uşi se află maşina şi nu va deschide acea uşă.
Prin evitarea uşii cu maşina, gazda furnizează informaţie privind uşa evitată. Odată ce această informaţie este furnizată, probabilitatea ataşată fiecărei uşi rămase nedeschise se schimbă.
Iată problema lui Monty Hall explicată într-un film cu Kevin Spacey (de la minutul 1:30). Videoclipul a fost sugerat pe FB de unul dintre cititori.
Cazul cu cinci uşi
Să ne imaginăm, pentru o înţelegere mai bună a problemei, că nu vorbim de trei uşi, ci de cinci uşi.
Probabilitatea să alegi ușa cu maşina din prima încercare este de una din cinci (1/5), adică de 20%. Asta înseamnă că probabilitatea ca ușa câștigătoare să fie una dintre celelalte patru este de 80%.
După ce gazda alege să deschidă trei uși necâștigătoare (cu capre) și să lase închisă doar o uşă, probabilitatea ca aceasta să ascundă maşina este de 80%.
Aşadar, da, decizia de a schimba opţiunea şi de a alege cealaltă uşă este cea care creşte şansele substanţial probabilitatea de a câştiga maşina.
· De unde numele de "Problema lui Monty Hall"?
Numele acestei probleme de logică are la bază un concursul televizat american intitulat "Let's Make a Deal", a cărui gazdă inițială a fost Monty Hall.
Surse: Wikipedia.org şi cartea The Outer Limits of Reason de Noson Yanofsky.
