Derivate ale funcţiilor uzuale

Ultimele intrebari pe QA

Tigara electronica
Tigari electronice
Y7.ro
Stiri

RSS 2.0

Participaţi la concursul "Medicina azi"! (06.02-25.05)! Citiţi regulamentul concursului.

Matematica

Scris de Adrian Bulat

Duminică, 27 Februarie 2011 10:31

În continuare, lista derivatelor pentru funcţiile uzuale.

Credit: http://www.hypercyber.it

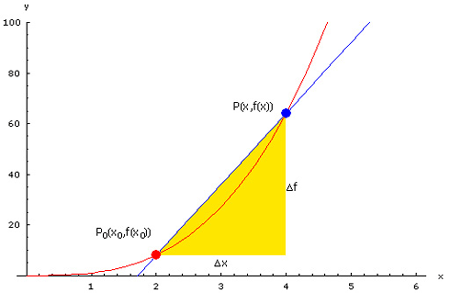
Derivata unei funcţii este o noţiune matematică ce a fost descoperită în jurul anului 1665 de Isaac Newton. Aceasta i-a permis să definească matematic noţiunea de viteză instantanee ca şi derivata faţă de timp a poziţiei în spaţiu în funcţie de timp, iar acceleraţia instantanee ca şi derivata în funcţie de timp a vitezei ca şi funcţie de timp.

Tabel cu derivate uzuale

$\begin{tabular}{|l|l|} $\displaystyleÂ a $ & $\displaystyle 0 $\\ $\displaystyle a x $ & $\displaystyle a $\\ $\displaystyleÂ \frac{1}{x} $ & $\displaystyle -\frac{1}{x^2} $\\ $\displaystyle \sqrt{x} $ & $\displaystyle \frac{1}{2 \sqrt{x}} $\\ $\displaystyle a x^n $Â & $\displaystyleÂ a n x^{n-1} $\\ $\displaystyle \sinÂ x $Â & $\displaystyleÂ \cos xÂ $\\ $\displaystyle \cos x $Â & $\displaystyle - \sin x $\\ $\displaystyle \tan x $Â & $\displaystyle \! \frac{1}{\cos^2 x} \,Â \! \rm{sau} \,Â 1+\tan^2 xÂ $\\ $\displaystyle \cot x$Â & $\displaystyleÂ \! -\frac{1}{\sin^2 x} \,Â \! \rm{sau} \,Â -1-\cot^2 x $\\ \end{tabular}$

$\begin{tabular}{|l|l|} $\displaystyle \arcsin x $Â & $\displaystyleÂ Â \frac{1}{\sqrt{1-x^2}} $\\ $\displaystyle \arccos x $Â & $\displaystyle -Â \frac{1}{\sqrt{1-x^2}} $\\ $\displaystyle \arctan x $Â & $\displaystyle \frac{1}{1+x^2} $\\ $\displaystyle a^x $Â & $\displaystyle a^xÂ \ln a $\\ $\displaystyle \ln \mid x\midÂ $Â & $\displaystyle \frac{1}{x} $\\ $\displaystyle e^x $Â & $\displaystyle e^x $\\ \end{tabular}$

Găsiţi în acest tabel: derivata funcţiei putere, derivata funcţiei exponenţiale, derivata funcţiei sinus, derivata funcţiei cosinus, derivata funcţiei tangentă, derivata funcţiei cotangentă, derivata funcţiei arcsin, derivata funcţiei arccos, derivat funcţiei arctan, derivata funcţiei logaritm, precum şi a altor funcţii uzuale. Acestea ţin de capitolul din matematică denumit analiză matematică.

Citeşte şi:

Derivate şi reguli de derivare (27-02-2011) Tabele de integrale nedefinite şi de primitive uzuale (26-02-2011) Graficele funcţiilor trigonometrice (13-03-2011) Funcţiile trigonometrice - o introducere (23-02-2011)

Adaugă comentariu

JComments

Ultimele mesaje pe forum

Probabilitate

Este numar natural multimea N incepe cu 0,iara zero e cardinalul multimii vide.Vad ca in unele contexte il exclud pe 0 si eu personal vad asta ca pe o idiotenie.De ce sa il excluzi pe 0 cand 0 are semnificatia sa clara ca numar.0 are rolul sau si e necesar sa il i...

mic exercitiu intelectual: geocentrism vs heliocentrism

Citat din mesajul lui: alexandru n. din Mai 16, 2012, 08:10:31 - experimentele lui Airy (numite convenabil de mainstream ”Airy’s failure”; de notat că George Airy era la rândul lui convins de heliocentrism, şi a pornit la acea experimentare cu gândul să demonstreze...

Problema: oglinda concava

Nu conteaza. Pozitia focarului este la o distanta de 0.5R atat fata de O cat si fata de O', nu? Se schimba doar semnul diferentei de sub modul.

Tangenta despre scrierile lui Ioan Damaschin

Citat din mesajul lui: AlexandruLazar din Ieri la 10:25:56 Eu sunt departe de a minimaliza importanța Sf. Ioan Damaschin în filosofia europeană; cu siguranță scrierile sale au fost un factor de progres, din păcate nu tocmai reprezentativ pentru Biserica acelor seco...

Scientia

Scientia terras irradiamus

Ultimele intrebari pe QA

Ultimele mesaje pe forum

SITEMAP • CONTACT• TERMENI ŞI CONDIŢII