Într-un articol recent am făcut o introducere a funcţiilor trigonometrice. Să vedem acum reprezentarea lor grafică şi explicaţiile de rigoare.

Introducere

Eşti la şcoală şi vrei să ai pe internet, în limba română, un referat de matematică cu o serie de tabele cu cele mai utile formule de matematică şi fizică? Echipa Scientia.ro face posibil acest lucru. Continuăm lecţiile de trigonometrie cu prezentarea graficelor funcţiilor sinus, cosinus, tangentă, cotangentă.

Detalii

de: Mihai Bărbulescu

Matematica

13 Martie 2011

Definiţia logaritmului

Fie {tex}a\in (0,\infty)-\{1\}{/tex} şi {tex}$b\in(0,\infty)${/tex}, două numere reale. Se numeşte logaritm al numărului real strict pozitiv {tex}$b${/tex} exponentul la care trebuie ridicat numărul {tex}$a${/tex}, denumit bază, pentru a obţine numărul {tex}$b${/tex}.

Notaţiile logaritmilor

Logaritmul numărului {tex}$b${/tex} în baza {tex}$a${/tex} se notează: {tex}$\log_a b${/tex}. Cu această notaţie şi cu definiţia de mai sus devine clar că {tex}$\displaystyle b=a^{\log_a b}${/tex}.

Funcţia logaritm şi graficul acesteia

Funcţia logaritm este, cu alte cuvinte, inversa funcţiei exponenţiale. Vom considera funcţia bijectivă {tex}$ f: \mathbb{R} \rightarrow (0, \infty) , f(x) = a^x ,  a \epsilon (0, \infty) - \{1\}${/tex}, al cărei grafic îl puteţi vedea în figura de mai jos:

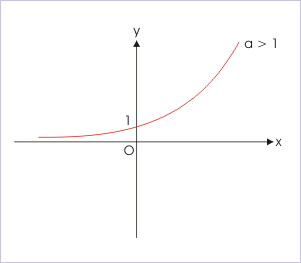
Acesta este graficul funcţiei exponenţiale. Observaţi că pentru o bază mai mare decât 1 are această figură. Observaţi că limita la minus infinit este 0, iar la plus infinit este chiar infinit.

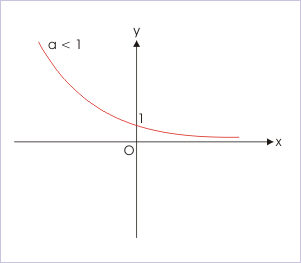
Acesta este graficul funcţiei exponenţiale a cărei baza este mai mică decât 1. Este vorba de o funcţie strict descrescătoare, spre deosebire de cealaltă, care era o funcţie strict crescătoare. De data aceasta, la minus infinit, funcţia tinde să fie infinită, pe când la infinit valoarea sa tinde către 0.

credit: e-formule.ro

Cazuri particulare de logaritmi

Logaritmii in baza 10 se numesc logaritmi zecimali şi se notează {tex}$\log_{10} b${/tex} sau {tex}$\lg b${/tex}, iar cei în baza e se numesc logaritmi naturali sau neperieni (de la numele matematicianului scoţian Neper, sau Napier, care i-a descoperit), şi se notează {tex}$\ln_a b${/tex}.

Proprietăţile logaritmilor

01. {tex}$\displaystyle \log_a x = \log_a y \Rightarrow x=y${/tex}, dacă {tex}$\displaystyle x, y>0${/tex} (injectivitatea funcţiei logaritm).

02. {tex}$ \displaystyle \log_a a=1${/tex}

03. {tex}$ \displaystyle \log_a 1=0${/tex}

04. {tex}$ \displaystyle \log_a x + \log_a y=\log_a (xy) ${/tex}

05. {tex}$ \displaystyle \log_a x-\log_a y=\log_a \left(\frac{x}{y}\right) ${/tex}

06. Fie {tex}$c\in \mathbb{R}$ {/tex}. Atunci {tex}$ \displaystyle \log_a x^c=c\cdot log_a x${/tex}

07. {tex}$ \displaystyle \log_a x\cdot \log_x a=1${/tex}

08. {tex}$ \displaystyle \log_a x=\frac{\log_y x}{\log_y a}${/tex}

09. {tex}$ \displaystyle a>1 , x \in (0,1) \Rightarrow \log_a x < 0 ${/tex}

10. {tex}$ \displaystyle a>1 , x>1 \Rightarrow \log_a x > 0 ${/tex}

11. {tex}$ \displaystyle a \in (0,1) , x \in (0,1) \Rightarrow \log_a x > 0 ${/tex}

12. {tex}$ \displaystyle a \in (0,1) , x>1 \Rightarrow \log_a x < 0 ${/tex}

13. Dacă {tex}$ \displaystyle a>1${/tex} funcţia {tex}$ \displaystyle f_a:\mathbb{R}^{+}-\{0\}} \rightarrow \mathbb{R}^{+}-\{0\}}, f_a (x)=\log_a x${/tex} este strict crescătoare, adică pentru {tex}$ \displaystyle x>y${/tex}, avem {tex}$ \displaystyle \log_a x>\log_a y${/tex}

14. Dacă {tex}$ \displaystyle a \in (0,1) ${/tex} funcţia {tex}$ \displaystyle f_a:\mathbb{R}^{+}-\{0\}} \rightarrow \mathbb{R}^{+}-\{0\}}, f_a (x)=\log_a x${/tex} este strict descrescătoare, adică pentru {tex}$ \displaystyle x>y${/tex}, avem {tex}$ \displaystyle \log_a x<\log_a y${/tex}

15. Fie {tex}$ \displaystyle c\in\mathbb{R}-\{0\}$ {/tex}. Atunci {tex}$ \displaystyle \log_{a^c} x=\frac{1}{c} \log_a x${/tex}

16. Fie {tex}$ \displaystyle  x\in\mathbb{R}, a>0, a\not=1${/tex}. Atunci {tex}$ \displaystyle a^x=e^{x \ln a}$ \displaystyle {/tex}.

Pentru fiecare dintre proprietăţile unde nu sunt puse condiţii pentru {tex}$ \displaystyle a, x, y ${/tex} , se subînţeleg condiţiile din definiţie.

Detalii

de: Laurenţiu Tuca

Matematica

13 Martie 2011

Prevederi introductive

1. Site-ul www.scientia.ro se supune legilor din România. Scientia asigură accesul liber la toate serviciile şi informaţiile destinate publicului disponibile pe platforma electronică www.scientia.ro. Deşi accesul la informaţii este liber, accesarea unora dintre informaţii se poate face în urma înregistrării pe site. Folosirea site-ului şi a informaţiilor trebuie să se realizeze în conformitate cu regulile stabilite în cuprinsul acestui text. Orice altă utilizare este interzisă.

Proprietatea intelectuală

2. Dreptul de proprietate intelectuală (copyright) pentru toate informaţiile existente pe acest site aparţine Scientia.ro, cu excepţia cazurilor în care se specifică altfel în conţinutul articolelor. Orice informaţii oferite de către vizitatorii site-ului devin parte integrantă a site-ului Scientia.ro şi nu pot fi şterse la cererea vizitatorilor, decizia privind păstrarea ori ştergerea oricărui text fiind dreptul exclusiv al proprietarilor Scientia. Nici un material de pe acest site nu poate fi preluat, vândut ori revândut, reprodus parţial, integral sau modificat fără permisiunea scrisă a Scientia. Articolele Scientia pot fi preluate, fără a fi nevoie de notificarea ori cererea dreptului de preluare, în limita a 500 de semne, dar nu mai mult de jumătate din conţinut, obligatoriu cu link către articolul original. Orice încălcare a acestor prevederi reprezintă încălcări ale legii 8/1996 privind drepturilor de autor şi drepturile conexe.  Logo-ul, stilul site-ului, precum şi informaţia furnizată prin site-ul Scientia.ro sunt proprietatea Scientia.ro sau a clienţilor săi.

Utilizatorii site-ului Scientia.ro sunt responsabili pentru informaţiile/materialele publicate pe site, fiind obligaţi să ţină cont de următoarele aspecte:
- sunt autorii informaţiilor/materialelor publicate;
- deţin drepturile de autor asupra acestora;
- au consimţământul titularului dreptului de autor pentru a publica respectivele informaţii/materiale.

Detalii

de: Iosif A.

Diverse

12 Martie 2011

Industria microcipurilor a sărbătorit pe 12 septembrie 53 de ani de la inventarea circuitului integrat. În general, un circuit electronic este alcătuit din componente electronice destul de voluminoase (rezistoare, condensatoare, bobine şi tranzistori) lipite pe o plăcuţă.

Detalii

de: Teodora Dan

Istoria ideilor şi a descoperirilor ştiinţifice

09 Martie 2011

Dacă Universul ar fi o prăjitură, cum l-aţi putea crea? Care este reţeta după care acesta a fost construit? Care sunt ingredientele de bază necesare? Pentru ca înţelegerea să fie deplină, vom face o scurtă trecere în revistă a descoperirilor importante privind ingredientele fundamentale.

Detalii

de: Adrian Buzatu

Istoria ideilor şi a descoperirilor ştiinţifice

03 Martie 2011

Zenon a fost un filozof grec presocratic, din sudul Italiei, membru al şcolii filozofice din Elea, întemeiată de Parmenide. Vă prezentăm în acest articol trei din cele mai cunoscute patru paradoxuri ale lui Zenon, unele dintre cele mai faimoase, mai durabile, mai şocante şi mai interesante paradoxuri, formulate de filozoful eleat în anul 450 î.Hr.

Filozoful grec Zenon, discipol al lui Parmenide, a trăit în secolul al cincilea î. Hr. şi ne-a lăsat moştenire câteva paradoxuri profunde a căror rezolvare ne invită să medităm asupra noţiunilor de infinit şi de mişcare. A fost numit de Aristotel fondatorul dialecticii (formă veche de găsire a adevărului, cunoscută şi drept arta interlocuţiunii).

Detalii

de: Mihai Bărbulescu

Matematica

03 Martie 2011

În continuare, lista derivatelor pentru funcţiile uzuale.

Credit: http://www.hypercyber.it

Derivata unei funcţii este o noţiune matematică ce a fost descoperită în jurul anului 1665 de Isaac Newton. Aceasta i-a permis să definească matematic noţiunea de viteză instantanee ca şi derivata faţă de timp a poziţiei în spaţiu în funcţie de timp, iar acceleraţia instantanee ca şi derivata în funcţie de timp a vitezei ca şi funcţie de timp.

Tabel cu derivate uzuale

{tex}
\begin{tabular}{|l|l|}
$\displaystyle  a $ & $\displaystyle 0 $\\
$\displaystyle a x $ & $\displaystyle a $\\
$\displaystyle  \frac{1}{x} $ & $\displaystyle -\frac{1}{x^2} $\\
$\displaystyle \sqrt{x} $ & $\displaystyle \frac{1}{2 \sqrt{x}} $\\
$\displaystyle a x^n $  & $\displaystyle  a n x^{n-1} $\\
$\displaystyle \sin  x $  & $\displaystyle  \cos x  $\\
$\displaystyle \cos x $  & $\displaystyle - \sin x $\\
$\displaystyle \tan x $  & $\displaystyle \! \frac{1}{\cos^2 x} \,  \! \rm{sau} \,  1+\tan^2 x  $\\
$\displaystyle \cot x$  & $\displaystyle  \! -\frac{1}{\sin^2 x} \,  \! \rm{sau} \,  -1-\cot^2 x $\\
\end{tabular}
{/tex}

{tex}
\begin{tabular}{|l|l|}
$\displaystyle \arcsin x $  & $\displaystyle   \frac{1}{\sqrt{1-x^2}} $\\
$\displaystyle \arccos x $  & $\displaystyle -  \frac{1}{\sqrt{1-x^2}} $\\
$\displaystyle \arctan x $  & $\displaystyle \frac{1}{1+x^2} $\\
$\displaystyle a^x $  & $\displaystyle a^x  \ln a $\\
$\displaystyle \ln \mid x\mid  $  & $\displaystyle \frac{1}{x} $\\
$\displaystyle e^x $  & $\displaystyle e^x $\\
\end{tabular}
{/tex}

Găsiţi în acest tabel: derivata funcţiei putere, derivata funcţiei exponenţiale, derivata funcţiei sinus, derivata funcţiei cosinus, derivata funcţiei tangentă, derivata funcţiei cotangentă, derivata funcţiei arcsin, derivata funcţiei arccos, derivat funcţiei arctan, derivata funcţiei logaritm, precum şi a altor funcţii uzuale. Acestea ţin de capitolul din matematică denumit analiză matematică.

Detalii

de: Adrian Bulat

Matematica

27 Februarie 2011

În acest articol, câte ceva despre noţiunea de derivată şi regulile de derivare:

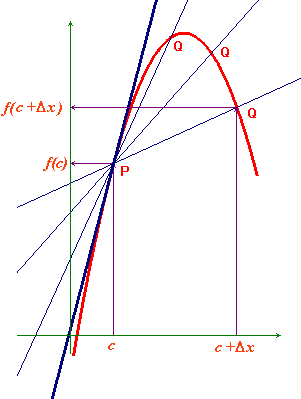
Credit: http://www.batmath.it

Reguli de derivare

{tex}
\begin{tabular}{|l|l|}
$\displaystyle \rm{Nume} $ & $\displaystyle \rm{Regula} $\\
$\displaystyle \rm{Liniara} $ & $\displaystyle ( af)^ \prime \! = a f^ \prime \! $\\
$\displaystyle \rm{Liniara} $ & $\displaystyle ( f + g)^ \prime \! = f^ \prime + g^\prime \! $\\
$\displaystyle \rm{Liniara} $ & $\displaystyle ( f - g)^ \prime \! = f^ \prime - g^\prime \! $\\
$\displaystyle \rm{Produs} $ & $\displaystyle ( f g )^ \prime \! = f^ \prime g + g^\prime f \! $\\
$\displaystyle \rm{Inversa} $ & $\displaystyle (\frac{1}{ f})^\prime = \frac{-f ^ \prime}{ f^2} $\\
$\displaystyle \rm{Coeficient} $ & $\displaystyle (\frac{f}{ g})^\prime = \frac{f ^ \prime g - f g^ \prime}{ g^2} $\\
$\displaystyle \rm{Compusa} $ & $\displaystyle ( g \circ f )^ \prime \! = (g^\prime \circ f )f^\prime \! $\\
$\displaystyle \rm{Reciproca} $ & $\displaystyle ( f ^{-1})^ \prime \! = \frac{1}{ f^\prime \circ f^{-1} } \! $\\
\end{tabular}
{/tex}

şi în particular regulile deduse pentru derivatele funcţiei compuse:

{tex}
\begin{tabular}{|l|l|}
$\displaystyle \rm{Putere}$ & $\displaystyle ( f ^ a)^ \prime \! =a f^{a - 1}f ^ \prime \! $\\
$\displaystyle \rm{Radical} $ & $\displaystyle (\sqrt{ f })^ \prime \! = \frac{f^\prime}{ 2 \sqrt {f} } \! $\\
$\displaystyle \rm{Exponentiala} $ & $\displaystyle (e^f )^ \prime \! = e^f f^ \prime $\\
$\displaystyle \rm{Logaritmica} $ & $\displaystyle (\log_{b} f)^ \prime = \frac{f^\prime}{ f \ln{b} } $\\
$\displaystyle \rm{Logaritmica} $ & $\displaystyle (\ln{f})^ \prime = \frac{f^\prime}{ f } $\\
\end{tabular}
{/tex}

În tabelul de mai sus găsiţi cele mai frecvente reguli utilizate la calcularea derivatelor. Pentru funcţiile care sunt exprimate ca o combinaţie liniară a funcţiilor simple, cum ar fi produs, cât sau compuse, folosim de asemenea un număr mic de reguli algebrice ce rezultă din definiţiile  de mai sus. Acestea ţin de ramura matematicii numită analiză matematică.

Detalii

de: Adrian Bulat

Matematica

27 Februarie 2011

În acest articol puteţi găsi lista primitivelor pentru câteva funcţii uzuale.

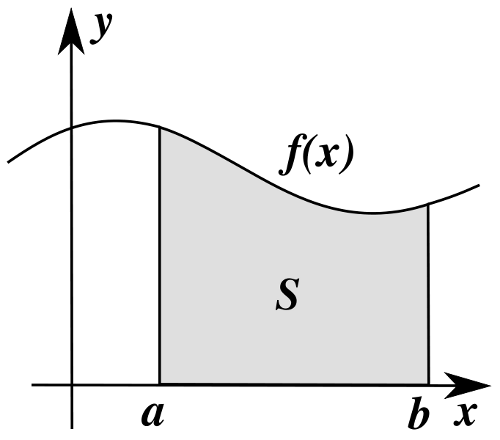
Credit: Wikimedia Commons

Tabel cu integrale uzuale

{tex}
\begin{tabular}{|l|l|}
\displaystyle \int \! x^n \, dx & \displaystyle \frac{x^{n+1}}{n+1} + C\\
\displaystyle \int \! a^x \, dx & \displaystyle \frac{a^x}{\ln a}+ C\\
\displaystyle \int \! \frac{1}{x} \, dx & \displaystyle \ln \mid x \mid + C\\
\displaystyle \int \! \frac{1}{x^2-a^2} \, dx & \displaystyle \frac{1}{2a} \ln \mid \frac{x-a}{x+a}\mid  + C\\
\displaystyle \int \! \frac{1}{x^2+a^2} \, dx  & \displaystyle \frac{1}{a} \arctan\frac{x}{a} + C \\
\displaystyle \int \! \sin x \, dx  & \displaystyle - \cos x+ C\\
\displaystyle \int \! \cos x \, dx  & \displaystyle  \sin x + C \\
\displaystyle \int \! \frac{1}{\cos^2 x} \, dx  & \displaystyle \tan x + C \\
\displaystyle \int \! \frac{1}{\sin^2 x} \, dx  & \displaystyle - \cot x + C \\
\end{tabular}
{/tex}

{tex}
\begin{tabular}{|l|l|}
$\displaystyle \int \! \tan x \, dx$  & $\displaystyle - \ln \mid\cos x\mid + C $\\
$\displaystyle \int \! \cot x \, dx$  & $\displaystyle \ln \mid \sin x\mid + C $\\
$\displaystyle \int \! \frac{1}{\sqrt{x^2+a^2}} \, dx$  & $\displaystyle \ln (x+\sqrt{x^2+a^2}) + C $\\
$\displaystyle \int \! \frac{1}{\sqrt{x^2-a^2}} \, dx$  & $\displaystyle \ln (x+\sqrt{x^2-a^2}) + C $\\
$\displaystyle \int \! \frac{1}{\sqrt{a^2-x^2}} \, dx$  & $\displaystyle \arcsin \frac{x}{a} + C $\\
\end{tabular}
{/tex}

Găsiţi în tabelele de mai sus primitivele pentru funcţia putere, funcţia exponenţială, funcţia 1/x, funcţia sinus, funcţia cosinus, funcţia tangentă, funcţia cotangentă, precum şi pentru alte funcţii uzuale.

Diferenţa între integrală nedefinită şi primitivă

Diferenţa între cele două noţiuni ar putea fi rezumată astfel:
Fie f:I->R(I interval din R), o funcţie care admite primitive.
Mulţimea tuturor primitivelor lui f se numeşte integrala nedefinită a funcţiei f.

Cf. Wikipedia, unii autori definesc integrala nedefinită a unei funcţii ca fiind mulţimea tuturor primitivelor posibile ale acesteia (varianta de mai sus). Alţii o definesc ca fiind un element ales arbitrar din acea mulţime.

Detalii

de: Adrian Buzatu

Matematica

26 Februarie 2011

Chimia nu este, de regulă, printre materiile preferate ale școlarilor. Dar chimia este un domeniu de studiu esențial pentru societatea modernă. În articolul de față doar prezentăm o serie de curiozități din acest domeniu, care nici măcar nu trebuie memorate :)

Ştiaţi că:

• numele hidrogenului înseamnă, la origine, „generator de apă"?

• corpul unui om de 70 de kg cuprinde 6 kg de hidrogen, 44 kg de oxigen şi 14 kg de carbon?

• metanul a fost descoperit de A. Volta în anul 1778 în mâlul bălţilor?

Detalii

de: Daniel Benea

Chimie

25 Februarie 2011

Cine sunt cei care au pus bazele radioului

Heinrich Rudolf Hertz a reuşit să transmită şi să recepţioneze primele unde radio între 1885 şi 1888, pe baza teoriei electromagnetismului a lui James Clerk Maxwell. James Clerk Maxwell a demonstrat matematic existenţa undelor electromagnetice în a doua jumătate a secolului al XIX-lea, fiind influenţat de cercetarea fenomenelor electromagnetice a lui Michael Faraday.

Hertz a construit un oscilator cu putere de transmitere a undelor radio, detectându-le cu un arc metalic (antena hertz – antena dipol). Când arcul se afla în interiorul câmpului electromagnetic al oscilatorului se produceau scântei. Asta demonstrează că undele electromagnetice au capacitatea nu numai de a fi transmise în spaţiu, ci şi de a fi detectate. Hertz nu a continuat însă transmisiunile, deoarece dorea să demonstreze teoria electromagnetismului, nu să dezvolte o cale de comunicare.

Cercetările și descoperirile lui Hertz l-au ajutat enorm pe Guglielmo Marconi, care a fructificat potenţialul utilizării acestor unde pentru a transmite mesaje cu ajutorul telegrafului (cunoscut azi ca fiind radio). În 1886, Marconi a realizat primele emisii radio sub forma unor mesaje codate, pe o rază de aproximativ 1,5 km. În 1899 a deschis prima fabrică ce producea aparate de telegraf fără fir în Chelmsford (Essex), stabilind totodată o legătură radio între Franţa şi Marea Britanie. Pentru descoperirea sa Marconi a obţinut premiul Nobel în fizică în 1909.

Nikola Tesla – inventatorul de drept al radioului

Cu patru ani înainte ca Marconi să inventeze radioul, Nikola Tesla inventase modelul teoretic al acestui aparat. În  1891, Tesla construise diferite aparate care produceau între 15000 şi 18000 de cicluri electromagnetice pe secundă. Energia de transmisie şi de radiaţie a frecvenţelor radio a fost o caracteristică expusă de către Tesla, care a susţinut că acestea pot fi utilizate pentru telecomunicaţii. După 1892, Tesla emis un raport de prezentare înaintea Instituţiei de Inginerie Electrică din Londra, în care el a sugerat că ar putea fi transmise mesaje fără fire. El a utilizat unde longitudinale, deoarece, în opinia sa, undele hertziene sunt o pierdere de energie.

După un proces pierdut cu Marconi în 1915 privind „paternitatea” radioului, Tesla avea să devină „părinte cu acte în regulă al radioului” în 1946, când Curtea Supremă din SUA i-a dat dreptate.

În România, în 1928 avea să fie lansat oficial primul semnal în eter de fizicianul Dragomir Hurmuzescu. Pe data de 18 decembrie 1928, Radiodifuziunea Română transmitea prima emisiune.

Radioul astăzi

Radioul a cunoscut mai multe evoluţii, de la radioul fix şi masiv până la radioul portabil cu tranzistori (inventat de Sony în 1954) sau diverse „device-uri” care au şi radio integrat (telefon, playere portabile etc.). Astăzi există în lume aproximativ 2,24 miliarde de aparate de radio.

Detalii

de: Mihai Bărbulescu

Istoria ideilor şi a descoperirilor ştiinţifice

25 Februarie 2011

Pendulul lui Foucault a constituit un experiment celebru pus în practică de către Jean Bernard Léon Foucault. Experimentul a confirmat rotaţia Pământului în jurul axei sale. A fost realizat pentru prima dată în faţa publicului în 1851, sub cupola Panteonului din Paris.

Detalii

de: Mihai Bărbulescu

Istoria ideilor şi a descoperirilor ştiinţifice

25 Februarie 2011

Eşti la şcoală şi vrei să ai pe internet, în limba română, o serie de tabele cu cele mai utile formule de matematică şi fizica? În acest articol vorbim despre formule de matematică necesare la liceu şi poate chiar la gimnaziu: funcţiile trigonometrice. Adică sinus, cosinus, tangentă, cotangentă şi relaţiile dintre ele.

Credit: Wikipedia.

Definiţii ale funcţiilor trigonometrice

Definiţia sinusului asociat unui unghi: raportul dintre lungimea catetei opuse unghiului respectiv şi lungimea ipotenuzei dintr-un triunghi dreptunghic.

Definiţia cosinusului asociat unui unghi: raportul dintre lungimea catetei alăturate unghiului respectiv şi lungimea ipotenuzei dintr-un triunghi dreptunghic .

Definiţia tangentei asociate unui unghi: raportul dintre lungimea catetei opuse unghiului respectiv şi lungimea catetei alăturate dintr-un triunghi dreptunghic.

Definiţia cotangentei asociate unui unghi: raportul dintre lungimea catetei alăturate unghiului respectiv şi lungimea catetei opuse dintr-un triunghi dreptunghic.

Relaţia de bază dintre sinus şi cosinus

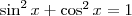
Formula tangentei în funcţie de sinus şi cosinus

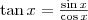
Formula cotangentei în funcţie de sinus şi cosinus

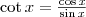
Tabel ale valorilor unghiurilor de bază în grade şi în radiani

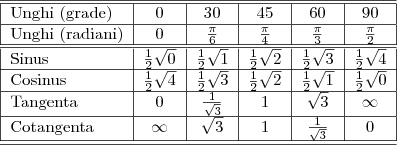
Aceste valori le puteţi găsi reprezentate şi pe acest cerc trigonometric, dar nu numai pentru valorile de la 0 la 90 de grade, precum mai sus în tabel, ci de la 0 la 360 de grade.

Valorile sinusului şi cosinusului pe cercul trigonometric.
Credit imagine: Wikipedia

Detalii

de: Adrian Buzatu

Matematica

23 Februarie 2011

Descoperirea curentului neutru al forţei slabe a fost realizată la laboratorul european CERN în anul 1973 şi a fost primul pas spre realizarea  unificării forţei electromagnetice şi a forţei slabe într-o singură forţă, forţa electroslabă.

Colaborarea Gargamelle, din cadrul laboratorului european CERN, a pus în funcţiune detectorul său de particule sub forma unei camere cu bule la începutul anilor ‘70, propulsând neutrini prin 12.000 litri de freon, un lichid greu. Aparatele de fotografiat au surprins imagini din diverse unghiuri ori de câte ori un impuls de neutrini traversa camera cu bule lungă de 5 metri.

Până în vara anului 1973, proiectul acumulase peste 700.000 de fotografii şi le distribuise celor şapte instituţii participante pentru a fi procesate. O armată de oameni, dintre care majoritatea femei, au scanat filmul pentru a căuta urmele lăsate sub formă de bule în lichidul freon exact pe unde treceau particulele subatomice încărcate din punct de vedere electric. Apoi, oamenii de ştiinţă au clasificat aceste urme şi au căutat semne ale unor noi tipuri de interacţiuni între neutrini, care nu mai fuseseră observate până atunci.

Fotografia de mai sus, surprinsă şi scanată în 1972, a atras atenţia oamenilor de ştiinţă ai grupului de analiză din Aachen, Germania, iar vestea s-a răspândit printre toţi colaboratorii. Particula neutrino, care nu lasă nicio urmă, deoarece nu are sarcină electrică, a pătruns în camera cu bule prin partea de jos a imaginii, ciocnindu-se de un electron.

Spre deosebire de toate celelalte cazuri cunoscute în prealabil, această coliziune nu a transformat neutrinul într-un alt tip de particulă. Particula a rămas tot neutrino după ce a lovit electronul, propulsându-l oarecum înspre stânga. Înaintând prin lichid, electronul a fost încetinit şi a început să emită lumină, cunoscută drept „bremsstrahlung” (germ. bremsen "a frâna" şi Strahlung "radiaţie"). Această lumină a creat apoi perechi electron-pozitron vizibile în fotografie, făcând ca electronul iniţial să poată fi cu uşurinţă identificat.

Aşadar, de ce s-au entuziasmat oamenii de ştiinţă? De mult timp, fizicienii au crezut că interacţiunile particulelor neutrino schimbă natura neutrinilor implicaţi. Aceste procese, ce implică forţa slabă, sunt numite curenţi încărcaţi electric ai forţei slabe, deoarece sunt intermediate de bosonii W cu o sarcină fie pozitivă, fie negativă. Dar spre sfârşitul anilor ‘60 şi începutul anilor ‘70, un grup de teoreticieni a dezvoltat o nouă descriere matematică pentru interacţiunile dintre neutrini, care impuneau particulelor neutrino o interacţiune slabă, dar printr-un curent neutru. Această interacţiune urma a fi mediată prin schimbul unei particule fără sarcină electrică, numită ulterior bosonul Z.

Rezultatele obţinute în urma experimentului Gargamelle au dovedit, fără urmă de îndoială, existenţa curentului neutru al forţei slabe, iar cercetătorii au început atunci să caute efectiv aceşti bosoni W şi Z prezişi de teoria care era astfel confirmată în mod indirect. Numărul din data de 3 septembrie 1973 al revistei “Physics Letters” a prezentat unul după altul două articole ale colaborării Gargamelle: unul despre interacţiunile curentului neutru al forţei slabe, bazate pe fenomenul prezentat mai sus, adică interacţionând cu electroni sau particule asemănătoare lor, numite leptoni; iar celălalt despre interacţiunile implicând curentul neutru ale neutrinilor, dar interacţionând cu nuclee sau particule asemenea lor, numite hadroni.

În anul 1974, experimentul E1A al laboratorului acceleratorului naţional Fermilab din Statele Unite a confirmat descoperirea. Teoria matematică ce prezisese existenţa curentului neutru al forţei slabe este acum cunoscută drept Modelul Standard al particulelor şi interacţiunilor elementare.

Articol tradus de Mălina Iorga din revista Symmetry, cu acordul editorului.

Detalii

de: Iosif A.

Istoria ideilor şi a descoperirilor ştiinţifice

22 Februarie 2011

În august 1982, Margaret Thatcher, pe atunci prim ministru al Marii Britanii, a realizat o vizită privată la laboratorul european CERN. La sosire, ea l-a rugat pe directorul general al CERN, Herwig Schopper, să o trateze cum ar trata un coleg om de ştiinţă. Aceasta deoarece şi doamna Thacher studiase chimia. Directorul i-a oferit un tur al laboratorului şi i-a povestit despre particulele purtătoare ale interacţiei nucleare slabe care erau căutate chiar atunci la laborator. Aceste particule erau denumite bozonii W şi Z şi erau cele ce permiteau dezintegrările nucleare care făceau, de exemplu, Soarele să strălucească.

Exemplu de eveniment care poate fi un bozon W.

La CERN, oamenii de ştiinţă operau două complexe subterane pentru a încerca detectarea acestor particule. Cele două detectoare erau denumite UA1 si UA2. Acestea colectau semnale provenite de la particulele create în urma coliziunilor proton-proton produse la laborator. Schopper i-a promis doamnei prim-ministru că o va informa de îndată ce vor fi fost descoperite aceste particule. Patru luni mai târziu, Schopper i-a trimis o scrisoare, împărtăşindu-i "în mod strict secret" vestea despre iminenta descoperire a bozonilor forţei nucleare slabe. El i-a explicat că oamenii de ştiinţă descoperiseră dezintegrarea bozonului W încărcat pozitiv într-un pozitron şi un neutrino (W⁺ -> e⁺ + v).

Scrisoarea pe care directorului laboratorului CERN o trimisese doamnei prim-ministru britanic Margaret Thatcher, în care o anunţa de iminenta descoperire a bozonului W.

Pe 25 ianuarie 1983, CERN a anunţat într-o conferinţă de presă descoperirea bozonului W. Detectoarele UA1 şi UA2 înregistraseră un total de nouă evenimente care arătau aşa cum ar arăta "semnătura" bozonului W. Particula era de mai bine de 15 ori mai grea decât oricare particulă elementară care fusese descoperită înainte.

La aproximativ patru luni după aceasta, CERN a anunţat şi descoperirea bosonului Z.

Citiţi şi articolul Descoperirea bozonului Z la CERN în 1983.

Articol tradus de Adrian Buzatu din revista Symmetry, cu acordul editorilor.

Detalii

de: Iosif A.

Istoria ideilor şi a descoperirilor ştiinţifice

22 Februarie 2011