Partea a 2-a a poveştii care prezintă epopeea care a durat mai bine de 300 de ani a demonstrării ultimei teoreme a lui Fermat. Aflaţi despre contribuţiile japonezilor Taniyama şi Shimura, dar şi despre finalizarea întreprinderii de către Andrew Wiles.
Marea teoremă a lui Fermat (1)
MATEMATICĂ LA SUPERLATIV
De aici totul se muta într-un alt domeniu al matematicii, fundamental diferit.
CURBELE ELIPTICE
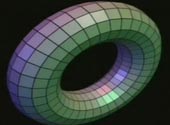
Curbele eliptice, deşi numele ar putea sugera astfel, nu sunt nici elipse şi nici măcar curbe, cel puţin nu în sensul obişnuit al cuvântului. Sunt de fapt nişte ecuaţii de forma y2 = x3 + ax2 + bx + c, unde a, b, c sunt numere întregi, a căror soluţie arată cam ca şi "gogoaşa" din imagine:
Curbă eliptică
Arată simplu, dar complexitatea lor aritmetică este imensă. Fiecare punct de pe "gogoaşă" reprezintă soluţia unei ecuaţii. Ele se numesc ecuaţii eliptice deoarece în trecut au fost folosite la măsurarea perimetrelor elipselor si lungimilor orbitelor planetare.
Provocarea ecuaţiilor eliptice constă în a stabili dacă ele admit ca soluţii numere întregi şi dacă da, câte. De exemplu, ecuaţia y2 = x3 -2, cu a=b=0 şi c=-2, are doar un set de soluţii întregi şi anume x=3 şi y=5, dar ca să demonstrezi că nu există şi alte soluţii este extrem de dificil. Problema poate fi simplificată dacă se stabileşte numărul soluţiilor în diferite aritmetici circulare. De exemplu, pentru curba eliptică x3 - x2 = y2 + y, numărul soluţiilor întregi pentru fiecare aritmetică circulară este:
L1 = 1 soluţie pentru 1 aritmetică
L2 = 4 soluţii pentru 2 aritmetici
L3 = 4 soluţii pentru 3 aritmetici
L4 = 8 soluţii pentru 4 aritmetici
............
Numărul de soluţii întregi pentru o aritmetică particulară formează L-seria ecuaţiei eliptice sau E-seria ecuaţiilor eliptice. Şi lista poate continua la infinit, astfel încât se pot obţine o mulţime de informaţii despre curba eliptică cu ajutorul L-seriilor.
FORMELE MODULARE
În paralel cu încercările de a stabili soluţiile unei ecuaţii eliptice, se desfăşura, într-un domeniu al matematicii fără aparent nici o legătură cu acestea, cercetări intense în domeniul formelor modulare.
Acestea sunt unele dintre cele mai abstracte entităţi matematice. Fiind entităţi cu o simetrie infinită, acestea pot fi permutate, comutate, interschimbate, reflectate şi rotite într-o infinitate de moduri şi rămân totuşi neschimbate.
O formă modulară este definită de 2 axe (x,y), dar axele sunt ambele complexe, adică fiecare axă are o parte reală (xr,yr) şi una imaginară (xi,yi),. Prin urmare, ele se reprezintă într-un spaţiu cu 4 dimensiuni numit spaţiu hiperbolic, care ar putea fi imaginat cam ca în figurile de mai jos (ca să fie percepute corect, ar trebui să vă curbaţi monitorul într-un astfel de spaţiu).
Formă modulară - exemplul 1
Formă modulară - exemplul 2
Formă modulară - exemplul 3
Formele modulare sunt diferenţiate de măsura în care fiecare formă şi mărime apare în ea, rezultând o serie modulară sau M-serie, o listă a ingredientelor şi a cantităţilor în care apar fiecare. Pe şleau, fiecărei forme modulare i se asociază o M-serie conţinând diferite informaţii (forme, mărimi, etc.).
Yutaka Taniyama
Tocmai cu studiul acestor forme modulare se ocupau nişte tineri japonezi, Yutaka Taniyama (deasupra) şi Goro Shimura (dedesubt).
Goro Shimura
Taniyama a examinat câteva forme modulare şi în fiecare caz M-seria unei forme modulare părea să corespundă perfect cu E-seria unei ecuaţii eliptice. Această ipoteză (în care a fost sprijinit numai de Shimura), care spune că orice curbă eliptică este modulară (sau că oricărei forme modulare i se poate asocia o ecuaţie eliptică) poartă numele de conjectura (părere bazată pe ipoteze sau pe presupuneri; prezumție, supoziție) Shimura-Taniyama. Mai trebuia însă să fie demonstrată.
LEGĂTURA
În 1984, matematicianul Gerhard Frey şi-a pus următoarea întrebare: ce s-ar întâmpla dacă teorema lui Fermat ar avea o soluţie până la urmă? Astfel el a arătat cum, pornind de la o soluţie fictivă pentru ecuaţie, poate face o curbă eliptică cu nişte proprietăţi foarte ciudate: pare să nu fie modulară! Problema este că Frey nu prea a dovedit că curba lui nu este modulară. Ideea lui a devenit conjectura epsilon, care a fost demonstrată ulterior de un alt matematician, Ken Ribet. Practic Frey a evidenţiat faptul că Teorema lui Fermat era departe de a fi doar o curiozitate nesemnificativă in teoria numerelor, ci era de fapt în strânsă legătură cu proprietăţile spaţiului.
Documentarul BBC Horizon intitulat "Fermat's last theorem" (eng.)
Aşadar:
1) Dacă conjectura Shimura-Taniyama poate fi dovedită, atunci orice curbă eliptică este modulară;
2) Dacă orice curbă eliptică trebuie să fie modulară, atunci curba eliptică a lui Frey nu poate exista;
3) Dacă curba eliptică a lui Frey nu există, nu pot exista nici soluţii la ecuaţia lui Fermat;
4) Prin urmare, Marea Teoremă a lui Fermat este adevărată.
Cea mai mare dificultate era demonstrarea conjecturii Taniyama-Shimura. Aceasta a fost contribuţia lui Andrew Wiles, care fusese fascinat de la vârsta de 10 ani de teorema lui Fermat. După 7 ani în care a lucrat închis în casă şi după o primă demonstraţie imperfectă, în 1995 închidea ultimul capitol, după mai bine de 300 de ani de la enunţarea teoremei.
Andrew Wiles
Cam asta ar fi, pe scurt, povestea ultimei teoreme a lui Fermat. Informaţii cuprinzătoare se găsesc pentru cine este interesat în fabuloasa carte a lui Simon Singh, "Marea Teorema a lui Fermat" - tradusă şi publicată şi în limba română de Editura Humanitas, în 2005. Există şi un documentar bine pus la punct, realizat tot de Simon Singh, în 1996, pentru seria Horizon de la BBC: Fermat's last theorem.
Sfârşit
