În acest episod vorbim despre întâlnirea lui Russell cu filozoful şi matematicianul Giuseppe Peano şi despre urmările acestei întâlniri asupra traseului intelectual al lui Russell. De asemenea, vorbim despre metoda folosită de Euclid în stabilirea bazelor geometriei.
PRINCIPIA MATHEMATICA
Interesul lui Russell în aceste probleme a început în anul 1900, la Primul Congres Internaţional al Filozofiei din Paris. Pe 3 august Russell l-a auzit pe filozoful şi matematicianul Giuseppe Peano vorbind la această întâlnire. El a fost aşa impresionat de claritatea minţii lui Peano, încât prezenţa la congres a reprezentat un moment de cotitură în cariera intelectuală a lui Russell. Acesta a crezut că abilităţile intelectuale ale lui Peano sunt produsul unei minţi care fusese disciplinată prin studiul logicii matematicii. Această claritatea fusese căutată de Russell de mulţi ani; s-a întors acasă, în Londra şi a început să studieze opera lui Peano.
În timp ce studia şi-a amintit de zilele în care era şcolar şi învăţa geometria, timp în care întreba despre fundamentele logice ale acestei ramuri a matematicii. Acum, împreună cu A.N.Whitehead, Russell s-a angajat într-o întreprindere majoră: să descopere fundamentele logice al matematicii. Acest proiect de mare amploare s-a concretizat în două volume cunoscute cu numele de Principia Mathematica.
Matematicienii au gândit poate înainte că erau riguroşi în ceea ce făceau; Russell şi alţii au indicat că, în interiorul argumentelor lor, matematicienii foloseau forme subtile de raţionare, uneori în mod inconştient, care nu fuseseră niciodată formulate în mod corect. Planul lui Russell a fost acela de a folosi o notaţie formală, simbolică în care toate regulile de inferenţă să fie totalmente explicite. Urma să fie:
- un sistem de semne;
- o gramatică; adică reguli pentru a combina semnele în formule;
- reguli de transformare care permit matematicienilor să treacă de la o formulă la alta;
- axiome;
- demonstraţii, implicând o secvenţă finită de formule, pornind cu o axiomă şi mergând apoi pas cu pas, folosind regulile de transformare.
NOŢIUNEA DE DEMONSTRAŢIE
Programul lui Russell presupunea punerea matematicii pe o structură logică, o idee ce mergea înapoi în timp până la Euclid. Vechii greci descoperiseră o mulţime de lucruri despre geometria lumii, dar Euclid a fost acela care a strâns aceste descoperiri într-o schemă logică şi consistentă în cartea Elementele Geometriei.
Euclid a început prin definirea celor mai simple elemente ale geometriei: punctele, liniile, planurile ş.a.m.d. Apoi a adăugat câteva axiome, care reprezintă punctele de plecare logice ale sistemului său şi erau aşa de evidente, spera Euclid, că trebuiau să fie în mod necesar adevărate. De exemplu, una dintre axiome ne spune că două linii paralele nu se întâlnesc, oricât de lungi ar fi acestea.
Pornind de aici, Euclid a căutat să demonstreze diferitele teoreme cunoscute ale geometriei, cum este de pildă faimoasa teoremă a lui Pitagora - pătratul ipotenuzei unui triunghi dreptunghic este egal cu suma pătratelor celorlalte două laturi (a catetelor).
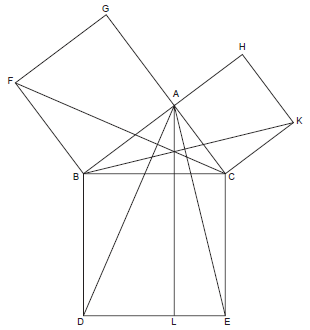
La baza abordării lui Euclid stă noţiunea de demonstraţie matematică. În demonstraţiile sale Euclid porneşte de la una dintre axiome şi construieşte un lanţ de afirmaţii, fiecare urmând-o în mod logic pe precedenta. În acest fel este posibil să ajungi la adevărul fiecărei teoreme folosind un număr mic de paşi şi folosind logica pentru a trece de la o etapa la alta. Demonstraţiile lui Euclid nu includ presupuneri ori ghiciri şi nici nu se bazează pe bun-simţ. Ele sunt construite cu o logică riguroasă.
Newton a folosit aceeaşi abordare în a măreaţă construcţie intelectuală "Principiile filozofiei naturale", în primul rând definind termenii de bază privind spaţiul, timpul ş.a.m.d, apoi adoptând un mic număr de axiome ca fiind "legile naturii". Înarmat cu toate acestea - şi demonstrând fiecare afirmaţie în mod logic, pas cu pas - Newton a fost capabil să stabilească adevăruri despre Univers.
Foarte interesant la aceste teoreme din sistemul lui Euclid este faptul că ele puteau fi demonstrate în mod logic pornind de la axiome, iar aceste teoreme puteau fi testate practic în lumea reală. Metoda lui Euclid a fost de importanţă cardinală, pentru că apela la logică, iar teoremele se potriveau cu experienţa. Teoremele sale erau adevărate şi în minte, şi aplicate pe teren.
Traducerea este făcută cu acordul autorului şi este protejată de legea drepturilor de autor.
