Teoria relativității: paradoxul miuonilor și dilatarea timpului

Paradoxul miuonilor (care, în fapt, nu este un paradox, după cum veți observa mai jos) este un exemplu fascinant care demonstrează dilatarea timpului, un concept fundamental în teoria relativității restrânse a lui Albert Einstein.

Fenomenul dilatării timpului a provocat dezbateri aprinse de-a lungul secolului al XX-lea, pe măsură ce teoria lui Einstein era dezbătută de fizicieni și filozofi, și a rămas una dintre cele mai elegante demonstrații experimentale ale relativității.

În acest articol, vom explora în detaliu aparentul paradox al miuonilor și vom explica modul în care dilatarea timpului funcționează în acest context.

Miuonii - particule efemere cu durata de viață extrem de scurtă

Miuonii sunt particule subatomice instabile, cu o masă de aproximativ 200 de ori mai mare decât cea a electronului. Ei sunt produși în mod natural atunci când razele cosmice, care provin din spațiu, lovesc atmosfera superioară a Pământului. Aceste raze cosmice interacționează cu nuclee atomice din atmosfera superioară, generând miuoni și alte particule.

Miuonii călătoresc cu viteze extrem de mari spre suprafața Pământului, dar au o durată de viață foarte scurtă. În repaus (în sistemul său de referință), un miuon trăiește în jur de 2,2 microsecunde înainte de a se dezintegra.

Având în vedere această durată de viață scurtă și distanța dintre atmosfera superioară și suprafața Pământului, care este de aproximativ 15 kilometri, ar fi de așteptat ca majoritatea miuonilor să se dezintegreze înainte de a ajunge la sol.

Totuși, un număr semnificativ de miuoni este detectat la nivelul solului. Această anomalie aparentă este ceea ce stă la baza paradoxului miuonilor și este un exemplu de dilatare a timpului.

Dilatarea timpului

Pentru a înțelege paradoxul miuonilor, trebuie să ne întoarcem rapid la conceptele de bază ale teoriei relativității restrânse. În conformitate cu această teorie, timpul și spațiul nu sunt constante universale, ci sunt relative, adică se schimbă în funcție de viteza relativă față de un observator.

La baza relativității restrânse stau două principii fundamentale:

1. Principiul relativității: legile fizicii sunt aceleași în toate sistemele de referință inerțiale, indiferent de viteza cu care se mișcă aceste sisteme unele în raport cu altele.

2. Viteza constantă a luminii: viteza luminii în vid este aceeași pentru toți observatorii, indiferent de viteza lor relativă sau de direcția de mișcare.

Unul dintre efectele cele mai interesante ale relativității restrânse este dilatarea timpului. Pentru un observator aflat în mișcare relativă față de altul, timpul va curge aparent mai lent. Cu cât viteza relativă a unui obiect este mai mare, cu atât dilatarea timpului este mai semnificativă.

Formula dilatării timpului

Pentru a înțelege acest fenomen matematic, trebuie să utilizăm formula dilatării timpului, care este derivată din teoria relativității restrânse:

Unde:

• Δt′ este timpul măsurat de un observator în mișcare (în acest caz, miuonul);
• $\Delta t$ este timpul măsurat de un observator staționar (de exemplu, un om de știință pe Pământ); 
• $v$ este viteza miuonului;
• $c$ este viteza luminii în vid.

Această formulă arată că, pe măsură ce viteza miuonului $v$ se apropie de viteza luminii $c$, termenul v²/c² se apropie de 1, iar valoarea lui √ (1−c²v²) devine foarte mică. Astfel, Δt′, adică timpul măsurat de observatorul aflat în mișcare (miuonul), crește semnificativ în raport cu Δt, timpul măsurat de un observator staționar.​

Dilatarea timpului și paradoxul miuonilor

Să analizăm modul în care acest efect este vizibil în cazul miuonilor care se formează la înălțimi mari în atmosferă. Călătorind cu viteze apropiate de cea a luminii (aproximativ 99,98% din viteza luminii), mionii ar trebui, în conformitate cu timpul lor propriu, să se dezintegreze înainte de a ajunge la sol, având în vedere durata lor de viață de doar 2,2 microsecunde. Totuși, din punctul de vedere al observatorilor de pe Pământ, mulți dintre acești mioni reușesc să ajungă la sol înainte de a se dezintegra.

Cum se explică acest fenomen?

Dacă un miuon călătorește la o viteză de aproximativ 0,998∗$c$ (unde $c$ este viteza luminii), dilatarea timpului poate fi calculată folosind formula:

Astfel, timpul pentru care miuonul pare să „trăiască” din perspectiva observatorului pe Pământ este extins de la 2,2 microsecunde la aproximativ 34,8 microsecunde. Aceasta înseamnă că miuonul poate parcurge o distanță mult mai mare decât ar fi de așteptat în baza duratei sale de viață normale. În cele 34,8 microsecunde, un miuon care călătorește cu aproape viteza luminii poate traversa o distanță de aproximativ 10,4 kilometri, ceea ce îi permite să ajungă la suprafața Pământului.

Viteza relativistă și efectele asociate

Pe lângă dilatarea timpului, relativitatea restrânsă mai include și un alt efect important: contracția lungimii. Conform acestei teorii, un obiect aflat în mișcare relativă față de un observator va apărea contractat de-a lungul direcției mișcării. În cazul miuonilor, contracția lungimii se aplică distanței pe care trebuie să o parcurgă până la sol.

Pentru un miuon, care se mișcă cu viteze apropiate de viteza luminii, distanța de 15 kilometri până la suprafața Pământului este „contractată” din perspectiva sa. Formula contracției lungimii este:

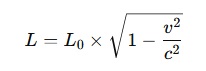
Unde:

• $L$ este lungimea măsurată de observatorul aflat în mișcare (miuonul);
• L₀​ este lungimea măsurată de un observator staționar (distanta până la sol, 15 km);
• $v$ este viteza miuonului;
• $c$ este viteza luminii.

Aplicând această formulă, miuonul percepe distanța de 15 kilometri ca fiind mult mai mică. Această contracție, împreună cu dilatarea timpului, permite miuonilor să ajungă la sol înainte de a se dezintegra. 

Testarea teoriei prin experimente 

Paradoxul miuonilor a fost testat în numeroase experimente, iar măsurătorile au confirmat cu precizie predicțiile teoriei relativității restrânse. Într-un experiment clasic realizat de Bruno Rossi și David Hall în anii 1940, cercetătorii au folosit detectoare de miuoni pentru a măsura numărul acestora la diferite altitudini. Ei au constatat că numărul miuonilor detectați la sol era mult mai mare decât s-ar fi așteptat în absența dilatării timpului.

Rezultatele experimentului au arătat că miuonii care călătoreau cu viteze foarte mari aveau un timp de viață aparent mai lung din perspectiva observatorilor de pe Pământ, validând astfel teoria relativității restrânse.

Concluzii

Paradoxul miuonilor este ilustrează unul dintre efectele cele mai surprinzătoare ale relativității restrânse: dilatarea timpului. Miuonii, cu durata lor de viață scurtă și vitezele extreme, reușesc să demonstreze cum timpul și spațiul nu sunt absolute, ci depind de viteza la care se mișcă un obiect în raport cu un observator. Fenomenele de dilatare a timpului și contracția lungimii sunt direct responsabile pentru capacitatea miuonilor de a ajunge la sol, în ciuda duratei lor de viață limitate.

Un videoclip care explică bine și exhaustiv paradoxul miuonilor, incluzând dilatarea timpului și contracția lungimii: