Scientia

O scurtă paralelă între teoriile newtoniene privind legităţile care descriu mişcarea corpurilor şi interpretarea ulterioară a mecanicii clasice introdusă de Pierre-Louis de Maupertuis şi cunoscută drept "principiul acţiunii minime", cu detalii inclusiv despre interpretarea dată de Richard Feynman acestui din urmă principiu.

Cât de ciudată este mecanica cuantică, partea I

MECANICA CLASICĂ ÎN ACŢIUNE

Când ne gândim cum planetele se deplasează pe orbită în jurul Soarelui, de obicei aderăm la viziunea lui Newton conform căreia acestea accelerează constant – în acest caz schimbându-şi direcţia de deplasare – sub acţiunea forţelor gravitaţionale. Plecând de la această idee putem calcula cu precizie traiectoriile planetelor, iar predicţia cu o acurateţe impresionantă a momentelor producerii eclipselor totale de Soare validează teoria.

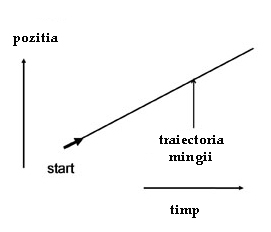
Figura 1. Mecanica clasică – viziunea lui Newton: mingea se deplasează pe o traiectorie rectilinie cu o viteză constantă, deoarece astfel se comportă corpurile atunci când nicio forţă nu acţionează asupra lor.

Există, totuşi, un alt mod de a gândi despre ceea ce se întâmplă în acest caz şi care oferă exact aceleaşi rezultate. În locul principiului acceleraţiei prin intermediul forţelor (să convenim că l-am putea numi aşa), există o alternativă care poartă numele de principiul acţiunii minime ori, mai corect, pincipiul lui Hamilton.  Este vorba despre un principiu formulat pentru prima oară la aproximativ 50 de ani după Newton, în cea mai timpurie formă a sa de către francezul Pierre Maupertuis, iar în cea mai recentă de către irlandezul William Rowan Hamilton.

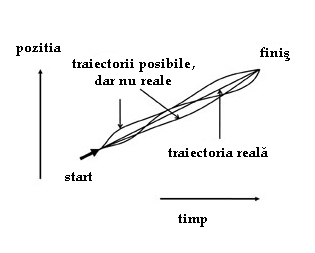
Figura 2. Mecanica clasică – viziunea lui Maupertuis: mingea se deplasează pe o traiectorie rectilinie cu viteză constantă pe toată lungimea parcursă, deoarece acesta este drumul corespunzător acţiunii minime între start şi sosire.

Ideea centrală este că atunci când o planetă se deplasează prin spaţiul cosmic ori atunci când o minge zboară prin aer, traiectoria urmată este una care minimizează o cantitate numită „acţiune” între punctele de start şi finiş. Acţiunea este în acest caz o mărime ce poate fi cuantificată pentru un anumit obiect în mişcare pe o anumită traiectorie. Ea este definită cu precizie şi măsurată în unităţi de energie multiplicate cu cele de timp. Detaliile sunt neimportante până în momentul în care e nevoie de efectuarea calculelor.

De aceea avem la dispoziţie două modalităţi diferite de a descrie situaţiile în fizica clasică, ambele la fel de eficace în ceea ce priveşte oferirea răspunsului corect. Pentru a da cel mai simplu răspuns posibil, ne putem gândi la o minge de golf care urmează o traiectorie ideală, în linie dreaptă şi fără a simţi efectele frecării cu solul. După Newton (figura 1), mingea se deplasează pe o traiectorie rectilinie uniformă, conformându-se legităţilor newtoniene. În viziunea lui Maupertuis (figura 2), mingea face acest lucru deoarece acest drum, cuprins între punctele de start şi finiş, este cel care are asociată valoarea minimă a mărimii pe care am numit-o „acţiune”. Acest exemplu banal poate fi mai interesant dacă terenul de golf nu mai este perfect plan, ci are cocoaşe şi gropi, adică prin introducerea în sistemul ales a unor forţe care acţionează asupra mingii. Cu toate acestea, principiile rămân acelaşi.

Principiul lui Hamilton este esenţialmente echivalent cu Legile lui Newton şi îşi dovedeşte utilitatea pe deplin atunci când oferă răspunsuri elegante pentru diverse tipuri de probleme clasice foarte complexe. Însă, prin prisma explicaţiei pe care o oferă, prezintă un defect major – pare că ne sugerează cumva că lucrurile trebuie să ştie încotro se deplasează înainte de a determina o modalitate de a ajunge acolo.

Privit dintr-o perspectivă diferită, acesta este în fapt punctul în care mecanica clasică face primul pas mare spre mecanica cuantică. Matematica principiului lui Hamilton poate fi descrisă folosind o formulare echivalentă astfel: cunoscând punctul de plecare şi mişcarea sa, un obiect va ajunge pe poziţii conectate de punctul de start printr-o traiectorie corespunzătoare unei acţiuni minime prin comparaţie cu cele asociate drumurilor vecine. Dacă se iau în considerare şi traiectorii mai depărtate de cea clasică, nu se va găsi o alta cu o acţiune asociată mai mică decât cea clasică.

Este o idee nefamiliară, necunoscută, dar merită să depunem puţin efort pentru a încerca să o înţelegem. O schimbare vitală de registru este cea dată de faptul că, deşi ne aflăm încă în regatul fizicii clasice, accentul se deplasează dinspre determinarea  drumului urmat de un obiect către găsirea unei modalităţi de a verifica validitatea ori, mai bine zis veridicitatea, traiectoriilor posibile. Iar factorul crucial este reprezentat de posibilitatea de a compara „acţiunile” asociate acestor diferite traiectorii.

Ceea ce conduce la o a treia imagine care descrie deplasarea mingii de golf, centrală pentru trecerea ulterioară către mecanica cuantică şi pe care o putem numi viziunea lui Feynman despre fizica clasică (figura 3).

Figura 3: Mecanica clasică – viziunea lui Feynman: mingea se deplasează pe o traiectorie care conţine punctele negre, care sunt şi coliniare, iar nu pe un drum care să treacă prin punctele albe, deoarece punctele negre sunt singurele care trec „testul acţiunii”. Iar asta înseamnă că există un drum de la punctul de start prin punctele negre a cărui acţiune asociată este minimă prin comparaţie cu cele asociate traiectoriilor vecine, şi nu există un asemenea drum de la punctul de start către punctele albe.

Dacă rămânem în zona fizicii clasice, putem alege să ignorăm această nouă şi stranie descriere rămânând la ideea mai confortabilă că lucrurile sunt accelerate de-a lungul traiectoriilor urmate de ele prin intermediul forţelor, numai că această abordare va reprezenta o preferinţă personală, iar nu una raţională. Noua viziune naşte întrebarea următoare: cum de ştiu lucrurile care dintre destinaţiile posibile sunt legate de punctul de start printr-un drum caracterizat de o valoare minimă a mărimii pe care am numit-o acţiune? Totuşi, e de menţionat şi faptul că viziunea veche, newtoniană, ridică întrebări la fel de dificile, precum: În ce mod răspund lucrurile acţiunii forţelor, astfel ca ele să fie accelerate doar cu valoarea necesară, clipă de clipă? Aşa cum vom vedea în continuare, versiunea care face uz de principiul acţiunii minime este cea pe care se pare că îşi bazează funcţionarea lucrurile din jurul nostru.

Cât de ciudată este mecanica cuantică? (3)

Textul de mai sus reprezintă traducerea articolului Why quantum mechanics is not so weird after all de Paul Quincey, traducere realizată cu acordul revistei Skeptical Inquirer.