
Fiind vacanţă, pentru câteva zile m-am dedicat cărţii de matematică de clasa a VIII-a. O bună introducere pentru mine şi sper că poate fi un bun rezumat pentru oricine are un interes în matematica de clasa a VIII-a.
Algebră
Intervale mărginite:
(a, b) = {x ∈ R | a < x < b} (interval deschis de extremităţi a şi b)
[a, b] = {x ∈ R | a ≤ x ≤ b} (interval închis de extremităţi a şi b)
[a, b) = {x ∈ R | a ≤ x < b} (interval închis la stânga în a şi deschis la dreapta în b)
(a, b] = {x ∈ R | a < x ≤ b} (interval deschis la stânga în a şi închis la dreapta în b)
Intervale nemărginite:
(a, +∞) = {x ∈ R | a < x} (interval deschis la stânga în a şi nemărginit la dreapta)
[a, +∞) = {x ∈ R | a ≤ x} (interval închis la stânga în a şi nemărginit la dreapta)
(-∞, a] = {x ∈ R | x ≤ a} (interval nemărginit la stânga şi închis la dreapta în a)
(-∞, a) = {x ∈ R | x < a} (interval nemărginit la stânga şi deschis la dreapta în a)
Formule de calcul prescurtat:
(x + y)2 = x2 + 2xy + y2
(x - y)2 = x2 - 2xy + y2
(x + y)(x - y) = x2 - y2
(x + y)3 = x3 + 3x2y + 3xy2 + y3
(x - y)3 = x3 - 3x2y + 3xy2 - y3
Produs cartezian. Produsul cartezian al mulţimilor A şi B este A x B = {(x, y) | x ∈ A şi y ∈ B}
Sisteme ortogonale de axe de coordonate:
Axa OX se numeşte axa absciselor.
Axa OY se numeşte axa ordonatelor.
Interioarele unghiurilor drepte se numesc cadrane.
Punctul O se numeşte originea sistemului de axe de coordonate.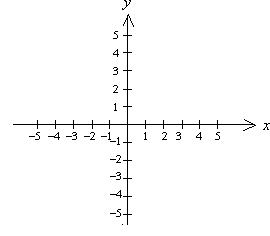
Noţiunea de funcţie.
Fiind date două mulţimi nevide, A şi B, şi o lege de corespondenţă f, care face ca fiecărui element x din A să-i corespundă un unic element y din B, spunem că am definit o funcţie pe A cu valori în B şi scriem f:A->B.
Graficul unei funcţii.
Fie o funcţie f:A->B. Prin graficul funcţiei f înţelegem mulţimea Gf = {(x, y) | x ∈ A şi y = f(x)}
Rezolvarea ecuaţiilor de forma ax = b şi ax + b = 0:
- Mulţimea soluţiilor ecuaţiei ax = b, x ∈ R (a ≠ 0) este S = {b/a}
- Mulţimea soluţiilor ecuaţiei ax + b = 0, x ∈ R (a ≠ 0) este S = {-b/a}
Ecuaţii de forma ax2 + bx + c = 0 (a ≠ 0):
- Rezolvarea formelor incomplete:
- Ecuaţia ax2 + bx = 0 (a, b ≠ 0, x ∈ R) se descompune în factori astfel x(ax + b) = 0, iar mulţimea soluţiilor S = {0; -b/a}
- Ecuaţia ax2 + c = 0 (a ≠ 0, x ∈ R) are trei situaţii. Dacă a şi c au acelaşi semn, atunci S = Ø, dacă c = 0, atunci S = {0}, sau dacă a şi c au semne diferite, atunci S = {-(-c/a)1/2; (-c/a)1/2}
- Pentru a rezolva în R ecuaţia ax2 + bx + c = 0 (a ≠ 0), calculăm numărul Δ = b2 - 4ac, numit discriminant. Dacă discriminantul este mai mic decât 0, ecuaţia nu are soluţie, dacă discriminantul este egal cu 0, S = {-b/2a}, iar dacă discriminantul este mai mare decât 0, S = {(-b-Δ1/2)/2a; (-b+Δ1/2)/2a}
Rezolvarea sistemelor de ecuaţii de forma:
ax + by = c
dx + ey = f
- Metoda grafică:
- Reprezentaţi în acelaşi sistem ortogonal de axe de coordonate dreptele soluţiilor celor două ecuaţii iar apoi determinaţi coordonatele punctului de intersecţie a dreptelor. Coordonatele reprezintă soluţia sistemului.
- Metoda substituţiei:
- Rezolvaţi o ecuaţie în raport cu o necunoscută (e.g ax + by = c => x = c - by/a), înlocuiţi în cealaltă ecuaţie obţinând o ecuaţie cu o singură necunoscută şi rezolvaţi ecuaţia. În final întoarceţi-vă la prima ecuaţie şi înlocuiţi cu soluţia de la a doua ecuaţie, iar apoi rezolvaţi.
- Metoda reducerii:
- Înmulţiţi convenabil fiecare termen (dintr-o ecuaţie sau din amândouă) cu acelaşi număr, adunaţi sau scădeţi cele două ecuaţii eliminând o necunoscută, iar apoi rezolvaţi ecuaţia rămasă.
Geometrie
Definiţii:
Poliedre - corpuri geometrice mărginite numai de feţe plane
Corpuri rotunde - corpuri geometrice mărginite parţial sau total de suprafeţe curbe (ne plane)
Piramida - fie S o suprafaţă poligonală şi V un punct exterior planului S. Reuniunea segmentelor [VM], unde M ∈ S, formează corpul geometric numit piramidă. Punctul V se numeşte vârful piramidei, iar poligonul S se numeşte baza piramidei.
Piramidă regulată - o piramidă care are baza poligon regulat şi muchiile laterale congruente
Apotema piramidei - distanţa de la vârf la o latură a bazei
Tetraedru - poliedrul cu cel mai mic număr de feţe (4 feţe)
Tetraedru regulat - un tetraedru cu toate muchiile congruente
Dreaptă perpendiculară pe plan - o dreaptă care este perpendiculară pe orice dreaptă din plan
Piciorul perpendicularei - punctul de intersecţie cu planul al unei perpendiculare
Distanţa de la un punct la un plan - lungimea segmentului care uneşte punctul cu piciorul perpendicularei duse din punctul dat pe plan
Înălţimea piramidei - distanţa de la vârful piramidei la planul bazei
Oblică - o dreaptă care intersectează un plan dar nu este perpendiculară pe plan
Piciorul oblicei - punctul de intersecţie cu planul al unei oblice
Distanţa dintre două plane paralele - lungimea unui segment cuprins între cele două plane şi perpendicular pe ele
Prisma - fie S o suprafaţă poligonală, inclusă într-un plan a, d o dreaptă care are un punct comun cu a, iar b un plan paralele cu a. Pentru fiecare punct M ∈ S se consideră dreapta care trece prin M, este paralelă cu d şi intersectează planul b într-un punct M'. Mulţimea formată din reuniunea tuturor segmentelor [MM'] se numeşte prismă.
Trunchi de piramidă - corpul geometric obţinut prin secţionarea unei piramide printr-un plan paralel cu baza, situat între bază şi planul de secţiune
Proiecţia ortogonală a unei figuri geometrice pe o dreaptă - mulţimea proiecţiilor punctelor acelei figuri pe dreaptă
Proiecţia unei figuri geometrice pe un plan - mulţimea proiecţiilor punctelor acelei figuri pe plan
Unghiul unei drepte cu un plan - unghiul format de către dreaptă şi proiecţia sa pe plan
Unghi diedru - figura geometrică formată de două semiplane delimitate de aceeaşi dreaptă
Aria totală a unei prisme = Aria laterală + 2 * Aria bazei
Volumul unei prisme = Aria bazei * Înălţimea prismei
Aria totală a unei piramide = Aria laterală + Aria bazei
Volumul unei piramide = (Aria bazei * Înălţimea piramide) / 3
Aria totală a unui trunchi de piramidă = Aria laterală + Aria bazei mari + Aria bazei mici
Volumul trunchiului de piramidă = [Înălţimea * (Aria bazei mari + Rădăcina pătrată din produsul ariilor celor două baze + Aria bazei mici)] / 3
Aria laterală a cilindrului circular drept = 2 * Pi * Raza bazei * Generatoarea
Aria totală a cilindrului circular drept = Aria laterală + 2 * Aria bazei
Volumul cilindrului circular drept = Pi * Pătratul razei bazei * Înălţimea
Aria laterală a conului circular drept = Pi * Raza bazei * Generatoarea
Aria totală a conului circular drept = Aria laterală + Aria bazei
Volumul conului circular drept = (Pi * Pătratul razei bazei * Înălţimea) / 3
Aria laterală a trunchiului de con circular drept = Pi * Generatoarea * (Raza bazei mari + Raza bazei mici)
Aria totală a trunchiului de con circular drept = Aria laterală + Pi * Pătratul razei bazei mari + Pi * Pătratul razei bazei mici
Volumul trunchiului de con circular drept = [Pi * Înălţimea * (Pătratul razei bazei mari + Pătratul razei bazei mici + Raza bazei mari * Raza bazei mici)] / 3
Aria sferei = 4 * Pi * Pătratul razei
Volumul sferei = (4 * Pi * Cubul razei) / 3
Axiome:
- Două puncte distincte determină o dreaptă
- Trei puncte ne coliniare determină un plan
- Dacă două puncte ale unei drepte aparţin unui plan, atunci dreapta este inclusă in plan
- Dacă două plane au un punct comun, atunci ele au o dreaptă comună
Determinarea planului:
- Trei puncte ne coliniare determină un plan
- O dreaptă şi un punct care nu-i aparţine determină un plan
- Două drepte paralele determină un plan
- Două drepte concurente determină un plan
Teoreme:
Teoremă privind dreapta paralelă cu un plan. O dreaptă paralelă cu o dreaptă din plan este paralelă cu planul sau conţinută în el
Teoreme de paralelism:
- Dacă o dreaptă d este paralelă cu un plan a şi conţinută într-un plan b care se intersectează cu planul a după o dreaptă g, atunci dreptele d şi g sunt paralele
- Dându-se două plane paralele, orice dreaptă dintr-un plan este paralelă cu al doilea plan
- Dacă două plane paralele sunt tăiate de un al treilea plan, atunci dreptele de intersecţie sunt paralele
- Dacă un plan conţine două drepte concurente paralele cu alt plan, atunci cele două plane sunt paralele
- Două plane paralele cu un al treilea plan (distinct de primele două) sunt paralele între ele
- Două plane paralele determină pe două drepte paralele, pe care le intersectează, segmente congruente
- Mai multe plane paralele determină pe două drepte oarecare, pe care le intersectează, segmente respectiv proporţionale
Criteriul de perpendicularitate - dacă o dreaptă este perpendiculară pe două drepte concurente dintr-un plan, atunci ea este perpendiculară pe plan
Teoreme de perpendicularitate şi paralelism:
- Două plane perpendiculare pe aceeaşi dreaptă sunt paralele
- Două drepte perpendiculare pe acelaşi plan sunt paralele
Teoreme privind oblicele:
- Perpendiculara dusă dintr-un punct pe un plan este mai scurtă decât orice oblică dusă din acel punct faţă de plan
- Două oblice, duse din acelaşi punct pe plan, sunt congruente atunci şi numai atunci când distanţele de la picioarele lor la piciorul perpendicularei sunt egale
Teoremă privind proiecţia unei drepte pe un plan - proiecţia unei drepte pe un plan este o dreaptă sau un punct
Teoremă privind proiecţia unui segment pe un plan - proiecţia unui segment pe un plan este un segment sau un punct
Teoremă privind lungimea proiecţiei unui segment - lungimea proiecţiei unui segment pe plan este egală cu lungimea segmentului înmulţită cu cosinusul unghiului format de dreapta suport a segmentului cu planul
Teorema celor trei perpendiculare - dacă o dreaptă este perpendiculară pe un plan şi prin piciorul acesteia trece o dreaptă conţinută în plan care este perpendiculară pe o altă dreaptă din plan, atunci orice dreaptă care uneşte un punct al perpendicularei pe plan cu punctul de intersecţie a celor două perpendiculare conţinute în plan, este perpendiculară pe a doua dreaptă din plan.

