În acest articol, câte ceva despre noţiunea de derivată şi regulile de derivare:
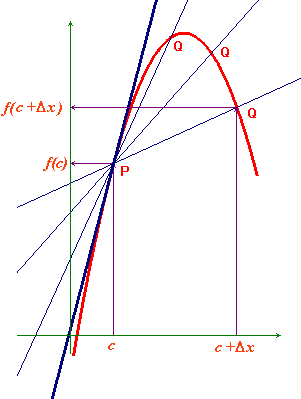
Credit: http://www.batmath.it
Derivata unei funcţii este o noţiune matematică ce a fost descoperită în jurul anului 1665 de către Isaac Newton. Metoda aceasta i-a permis să definească matematic noţiunea de viteză instantanee ca derivata în funcţie de timp a poziţiei în spaţiu în funcţie de timp, iar acceleraţia instantanee ca şi derivata în funcţie de timp a vitezei ca şi funcţie de timp. Nu toate funcţiile admit însă derivată, de pildă ele neavând derivată în punctele de discontinuitate, de întoarcere sau cele în care au o tangentă verticală.
Reguli de derivare
{tex}
\begin{tabular}{|l|l|}
$\displaystyle \rm{Nume} $ & $\displaystyle \rm{Regula} $\\
$\displaystyle \rm{Liniara} $ & $\displaystyle ( af)^ \prime \! = a f^ \prime \! $\\
$\displaystyle \rm{Liniara} $ & $\displaystyle ( f + g)^ \prime \! = f^ \prime + g^\prime \! $\\
$\displaystyle \rm{Liniara} $ & $\displaystyle ( f - g)^ \prime \! = f^ \prime - g^\prime \! $\\
$\displaystyle \rm{Produs} $ & $\displaystyle ( f g )^ \prime \! = f^ \prime g + g^\prime f \! $\\
$\displaystyle \rm{Inversa} $ & $\displaystyle (\frac{1}{ f})^\prime = \frac{-f ^ \prime}{ f^2} $\\
$\displaystyle \rm{Coeficient} $ & $\displaystyle (\frac{f}{ g})^\prime = \frac{f ^ \prime g - f g^ \prime}{ g^2} $\\
$\displaystyle \rm{Compusa} $ & $\displaystyle ( g \circ f )^ \prime \! = (g^\prime \circ f )f^\prime \! $\\
$\displaystyle \rm{Reciproca} $ & $\displaystyle ( f ^{-1})^ \prime \! = \frac{1}{ f^\prime \circ f^{-1} } \! $\\
\end{tabular}
{/tex}
şi în particular regulile deduse pentru derivatele funcţiei compuse:
{tex}
\begin{tabular}{|l|l|}
$\displaystyle \rm{Putere}$ & $\displaystyle ( f ^ a)^ \prime \! =a f^{a - 1}f ^ \prime \! $\\
$\displaystyle \rm{Radical} $ & $\displaystyle (\sqrt{ f })^ \prime \! = \frac{f^\prime}{ 2 \sqrt {f} } \! $\\
$\displaystyle \rm{Exponentiala} $ & $\displaystyle (e^f )^ \prime \! = e^f f^ \prime $\\
$\displaystyle \rm{Logaritmica} $ & $\displaystyle (\log_{b} f)^ \prime = \frac{f^\prime}{ f \ln{b} } $\\
$\displaystyle \rm{Logaritmica} $ & $\displaystyle (\ln{f})^ \prime = \frac{f^\prime}{ f } $\\
\end{tabular}
{/tex}
În tabelul de mai sus găsiţi cele mai frecvente reguli utilizate la calcularea derivatelor. Pentru funcţiile care sunt exprimate ca o combinaţie liniară a funcţiilor simple, cum ar fi produs, cât sau compuse, folosim de asemenea un număr mic de reguli algebrice ce rezultă din definiţiile de mai sus. Acestea ţin de ramura matematicii numită analiză matematică.
