Scientia

Vreme de 358 de ani, marii matematicieni ai lumii au încercat în zadar să găsească demonstraţia teoremei lui Fermat, devenită între timp simbol al misterului matematic. Citiţi în continuare povestea unuia dintre cele mai frumoase raţionamente realizate vreodată.

MAREA TEOREMĂ A LUI FERMAT - MATEMATICA LA SUPERLATIV

PIERRE de FERMAT ŞI ORIGINILE TEOREMEI

"Am descoperit o demonstraţie cu adevărat minunată, dar nu am aici destul spaţiu pentru a o scrie."

Acestea sunt cuvintele notate de ilustrul matematician Pierre de Fermat pe marginea unei pagini din ediţia Aritmeticii lui Diofant, în 1637. De aici a început nebunia. Vreme de 358 de ani, marii matematicieni ai lumii au încercat în zadar să găsească demonstraţia teoremei lui Fermat, devenită simbol al misterului matematic. Când o generaţie capitula, următoarea devenea mai îndârjită şi mai hotărâtă. Pentru matematică, importanţa teoremei consta în faptul că prin încercarea de a o demonstra au fost făurite noi metode puternice care au dus la crearea unei vaste ramuri a matematicii - "teoria algebrică a numerelor". Totul a fost cu atât mai frustrant, cu cât totul se baza pe un enunţ atât de simplu, încât şi un elev de clasa a VIII-a îl putea înţelege.

Originile teoremei pornesc de la şi mai celebra teoremă a lui Pitagora, care ne spune că într-un triunghi dreptunghic, pătratul ipotenuzei este egal cu suma pătratelor catetelor, adică:

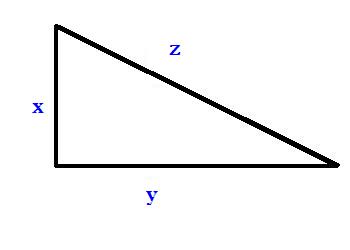
x² + y² = z²

3² + 4² = 5²

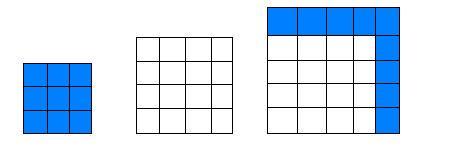
Două pătrate însumate formează un al treilea pătrat. De exemplu: 9+16=25.

Ca urmare a formulării clare şi concise a lui Pitagora, teorema a fost memorată şi reţinută o viaţă întreagă de milioane, dacă nu miliarde de minţi omeneşti. Este teorema fundamentală pe care orice şcolar este obligat s-o înveţe. Dar, în ciuda faptului că poate fi înţeleasă de un puşti de zece ani, creaţia lui Pitagora a fost sursa de inspiraţie pentru o problemă care a biruit cele mai mari minţi matematice ale tuturor timpurilor.

Dar ce se întâmplă dacă ridicăm pe x,z şi z la puterea a 3-a?  Adică dacă avem x³ + y³ = z³ ? Rezultă ceva de genul:

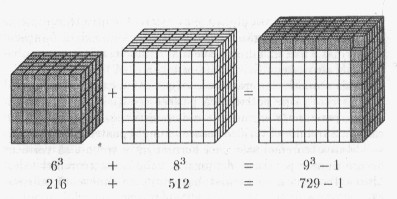
În acest caz un cub 6x6x6 adunat cu un cub 8x8x8 nu se potriveste perfect , neavând suficiente blocuri pentru a forma un cub 9x9x9.
Imagine - Marea Teorema a lui Fermat  - Simon Singh (Ed Humanitas - 2005)

Se pare că nu există soluţii pentru această ecuaţie. La fel cum nu există pentru x⁴ + y⁴ = z⁴, x⁵ + y⁵ = z⁵ şi, de fapt, pentru xⁿ + yⁿ = zⁿ.

Prin urmare teorema enunţată de Fermat, sună cam aşa:
Ecuaţia xⁿ + yⁿ = zⁿ nu are soluţii întregi diferite de zero, pentru n mai mare ca 2.
Complicat? Deloc. Dar acest lucru trebuie demonstrat. Aici se schimbă lucrurile radical.

CAZURI PARTICULARE

Cazul n=4 admite o demonstraţie elementară, schiţată de Fermat însuşi. El a folosit metoda coborârii infinite. Pentru a demonstra că nu există soluţie pentru această ecuaţie el a presupus că există o soluţie ipotetica (x1,y1,z1) cu proprietatea ca e minima. Atunci se demonstrează că există o soluţie şi mai mică decât aceasta, de unde apare contradicţia.
După aproximativ 100 de ani, Euler vine cu o demonstrație pentru cazul n=3, demonstrație care, de fapt, conținea o greșeală, corectată ulterior de alți matematicieni.  Pentru a extinde demonstrarea teoremei de la n=4 la n=3 Euler introduce "bizara noţiune" de număr imaginar.
În 1825, francezii Johann Peter Gustav Lejeune Dirichlet şi Adrien-Marie Legendre tranşează cazul n=5, demonstraţia având ca punct de plecare o idee mai veche a lui Sophie Germain.
În 1839 Gabriel Lamé a demonstrat teorema lui Fermat pentru n=7. El a fost precedat de Dirichlet care a demonstrat teorema pentru exponentul 14 în 1832. Demonstraţia pentru n=14 este însă mult mai uşoara decât pentru n=7. În 1840 Henri Lebesgue a găsit o demonstraţie mult mai simplă decât cea a lui Lame.

La mijlocul secolului XIX, Academia Franceză instituie un premiu de 3000 franci (o sumă enormă atunci) pentru o demonstraţie completă a teoremei.  În 1908, magnatul german Paul Wolfskehl alocă uriaşa sumă de 100.000 de mărci celui ce va demonstra teorema ('oferta' fiind valabilă până în 2007), ceea ce are ca efect apariţia a numeroase demonstraţii cu erori mai mult sau mai puţin evidente.  Deşi se progresa extrem de încet, era încurajator totuşi faptul că orice demonstraţie care funcţionează pentru n=4 funcţionează şi pentru n=8,12,16,20 (şi alţi multiplii de 4). De asemenea o demonstraţie pentru n=3 funcţionează şi pentru cazurile n=6,9,12,15.

Oricum, odată cu apariţia calculatoarelor teorema s-a rezolvat până la n=10.000 , apoi până la n=25.000 , astfel încât până în 1980 erau elucidate toate cazurile cu n<4.000.000.  În ultimii ani de dinaintea găsirii demonstraţiei complete pentru orice n>2, matematicienii erau convinşi că prin metode elementare nu se mai poate aduce nimic nou.

Marea teoremă a lui Fermat (2)

Autor: Mădălin Filip