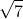Lungimea unui segment

Question

În triunghiul echilateral ABC cu latura de 6radicaldin3 cm, punctul M este mijlocul laturii BC. Fie D simetricul punctului A faţă de B, DM  AC = {P} şi N mijlocul segmentului AP. Aflaţi lungimea segmentului BN.

Answer 1

AB = BC = AC = BD = 6 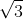^. = a

AN = AP  ;  BM = MC = a / 2

Trasăm segmentele DC și BF AC

În triunghiul isoscel 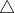BDC segmentul BF este înălțime, mediană și bisectoare, iar DM este mediană. Deci punctul E este centrul de greutate (intersecția medianelor) și este situat la 1/3 de bază și 2/3 de vârf. Adică EF = BF / 3  

În triunghiul dreptunghic 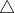BFC (cu unghiul BCF = 30⁰) BF = BC / 2 = a / 2 . Deci EF = a / 6

DF² = BD² – BF² = a ² – (a / 2) ² = 3 a ² / 4

DE² = DF² + EF² = 3 a ² / 4 + a ² / 36 = 28 a ² / 36 = 7 a ² / 9

DE = (a / 3 ) ^.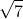

În triunghiul 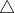ADP segmentul BN este linie mijlocie. Deci BN PE. Și cum BE NP înseamnă că BEPN este paralelogram. Deci BE = NP = AN. Dar cum și AB = BD și unghiurile BAN și DBE sunt egale, atunci triunghiurile 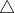BAN și 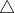DBE sunt egale. Deci:

DE = BN = (a / 3) 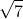^. = 2 ^.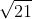

Am mai găsit două soluții, dar și ele sunt bazate pe teorema lui Pitagora. Ar fi interesantă o rezolvare fără această teoremă. De exemplu doar pe baza asemănării triunghiurilor. Totuși pare puțin probabilă datorită acelui

Comments

Dacă nu ne plac triunghiurile dreptunghice (teorema lui Pitagora, sinusuri, etc.) și nici teorema cosinusului și fără BF, se arată că AC este împărțită în trei părți egale de punctele N și P (teorema lui Menelaus), iar apoi BN se calculează cu formula medianei în funcție de laturile triunghiului. Asta dacă se dorește o soluție care să conțină elemente relativ mai puțin utilizate.