Considerand 0 pe axa x la mijlocul caramizii de suport, as calcula astfel coordonata x a centrului de masa a subturnului stabil format din (n-1) caramizi (fiind vorba de caramizi identice, se ajunge la suma coordonatelor pe axa x a centrelor de masa individuale, impartita la numarul de caramizi):
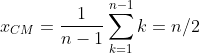
Raportat la lungimea caramizilor, L=20, aceasta coordonata nu trebuie sa depaseasca valoarea L/2, lucru care se intampla, dupa calculele mele, cand n atinge valoarea 21. Avem un echilibru la limita cand ajungem la 20 de caramizi, iar la a 21-a turnul se prabuseste in mod cert.