Nu am inteles exact daca asteptati sa vina elevii cu o rezolvare sau asteptati o rezolvare pentru elevi. In a doua situatie, varianta mea este urmatoarea:
Notam f, g,q, r, deimpartitul,impartitorul, catul si respectiv restul.
f=gq+r , f=r pentru g=0
Se face substitutia 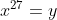 ,
, 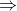
 ,
,
 ,
,
 ,unde r(y) are forma
,unde r(y) are forma
 , deoarece gr(r(y))<gr(g(y))=3
, deoarece gr(r(y))<gr(g(y))=3
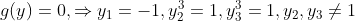 ,
,

 ,
,

 ,
,
 ,
,
 ,
,
rezolvand sistemul ,folosind relatiile lui Viete.....



rezulta a=1, b=1, c=1 si
 ,
,
