Răspunsul lui AdiJapan este foarte corect, dar există o ciudățenie , dacă putem s-o numim așa, care atribuie cercului, cu ghilimele corespunzătoare, proprietatea de poligon regulat.
Este vorba despre o formulă generală pentru arie : 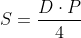 ,
,
unde D este diametrul cercului înscris în poligonul regulat, iar P este perimetrul poligonului.
Acest lucru se demonstrează în felul următor.
Din fiecare vârf al unui poligon regulat cu n laturi se trasează perpendiculara pe mijlocul laturii opuse dacă poligonul are un număr impar de laturi sau în vârful opus dacă are un număr par de laturi și se obțin 2n triunghiuri dreptunghice congruente.
Cateta mică a unui astfel de triunghi este raza cercului înscris în poligon, iar cateta mare este jumătate din lungimea l a laturii poligonului, iar suprafața unui triunghi va fi 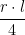 .
.
În acest fel suprafața poligonului va fi
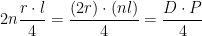
În cazul cercului, D este exact diametrul cercului, iar P este lungimea L a cercului,
iar suprafața cercului va fi 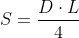 , adică un sfert din produsul diametrului și lungimii cercului.
, adică un sfert din produsul diametrului și lungimii cercului.
De altfel, la acest rezultat se poate ajunge și în modul următor :
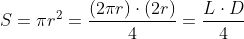 .
.