Intradevar este un sistem de olimpiada ce necesita clasa a 11 finalizata.
Sa scriem sistemul sub alta forma.
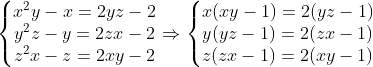
Acuma apare o discutie pentru cazurile in care factori respectivi sunt nuli.Sa observam ca nu putem avea x,y sau z nuli.Daca x=0 din prima relatie obtinem yz=1 si in a doua relatie vom obtine 0=-2 deci absurd.La fel si pentru y sau z egali cu 0 .Daca xy-1=0 vom obtine din prima relatie yz-1=0 si din a doua zx-1=0 si verifica si a treia ecuatie.Adica obtinem un sistem simplu xy=yz=xz=1 cu solutiile x=y=z=1 sau -1.Sa presupunem acma ca acei factori sunt diferiti de 0 adica xy,xz si yz diferiti de 1.inmultim cele 3 ecuatii si dupa simplificare obtinem xyz=8.In acest caz vom transforma ecuatiile astfel:
 Sa consideram functia
Sa consideram functia

avem derivata  deoarece delta numaratorului e negativ.Deci f este descrescatoare.
deoarece delta numaratorului e negativ.Deci f este descrescatoare.
Deci avem y=f(x),z=f(y),x=f(z).
Daca x>y atunci f(x)<f(y) adica y<z de unde f(y)>f(z) adica z>x de unde f(z)<f(x) adica x<y contradictie.Deci x=y adica f(x)=f(z) deci x=z in concluzie x=y=z si cum xyz=8 mai obtinem solutia x=y=z=2.