Daca am inteles bine formularea problemei,raspunsul ar putea fi:
X are 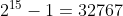 submultimi nevide, acestea putand avea suma elementelor cuprinsa intre 1 si ( 2003+2004+...2017)=30150. Cum 32767
submultimi nevide, acestea putand avea suma elementelor cuprinsa intre 1 si ( 2003+2004+...2017)=30150. Cum 32767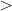 30150, conform principiului cutiei lui Dirichlet, exista 2 submultimi ale lui X care sa aiba aceeasi suma a elementelor. Daca cele 2 submultimi gasite nu sunt disjuncte, se elimina elementele comune si se obtin 2 submultimi disjuncte A si B astfel incat suma elementelor lui A si B sa fie egale .
30150, conform principiului cutiei lui Dirichlet, exista 2 submultimi ale lui X care sa aiba aceeasi suma a elementelor. Daca cele 2 submultimi gasite nu sunt disjuncte, se elimina elementele comune si se obtin 2 submultimi disjuncte A si B astfel incat suma elementelor lui A si B sa fie egale .
Pentru pct.2 X= {1,2,4,8,16,32,64,128,256,512,1024}