Definiţia logaritmului
Fie {tex}a\in (0,\infty)-\{1\}{/tex} şi {tex}$b\in(0,\infty)${/tex}, două numere reale. Se numeşte logaritm al numărului real strict pozitiv {tex}$b${/tex} exponentul la care trebuie ridicat numărul {tex}$a${/tex}, denumit bază, pentru a obţine numărul {tex}$b${/tex}.
Notaţiile logaritmilor
Logaritmul numărului {tex}$b${/tex} în baza {tex}$a${/tex} se notează: {tex}$\log_a b${/tex}. Cu această notaţie şi cu definiţia de mai sus devine clar că {tex}$\displaystyle b=a^{\log_a b}${/tex}.
Funcţia logaritm şi graficul acesteia
Funcţia logaritm este, cu alte cuvinte, inversa funcţiei exponenţiale. Vom considera funcţia bijectivă {tex}$ f: \mathbb{R} \rightarrow (0, \infty) , f(x) = a^x , a \epsilon (0, \infty) - \{1\}${/tex}, al cărei grafic îl puteţi vedea în figura de mai jos:
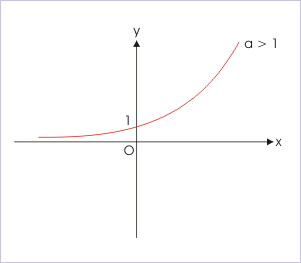
Acesta este graficul funcţiei exponenţiale. Observaţi că pentru o bază mai mare decât 1 are această figură. Observaţi că limita la minus infinit este 0, iar la plus infinit este chiar infinit.
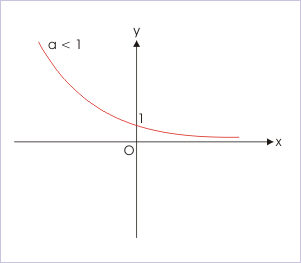
Acesta este graficul funcţiei exponenţiale a cărei baza este mai mică decât 1. Este vorba de o funcţie strict descrescătoare, spre deosebire de cealaltă, care era o funcţie strict crescătoare. De data aceasta, la minus infinit, funcţia tinde să fie infinită, pe când la infinit valoarea sa tinde către 0.
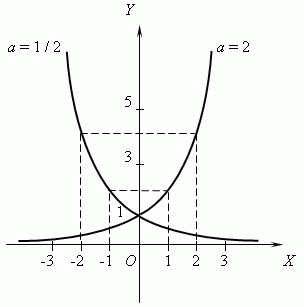

credit: e-formule.ro
Cazuri particulare de logaritmi
Logaritmii in baza 10 se numesc logaritmi zecimali şi se notează {tex}$\log_{10} b${/tex} sau {tex}$\lg b${/tex}, iar cei în baza e se numesc logaritmi naturali sau neperieni (de la numele matematicianului scoţian Neper, sau Napier, care i-a descoperit), şi se notează {tex}$\ln_a b${/tex}.
Proprietăţile logaritmilor
01. {tex}$\displaystyle \log_a x = \log_a y \Rightarrow x=y${/tex}, dacă {tex}$\displaystyle x, y>0${/tex} (injectivitatea funcţiei logaritm).
02. {tex}$ \displaystyle \log_a a=1${/tex}
03. {tex}$ \displaystyle \log_a 1=0${/tex}
04. {tex}$ \displaystyle \log_a x + \log_a y=\log_a (xy) ${/tex}
05. {tex}$ \displaystyle \log_a x-\log_a y=\log_a \left(\frac{x}{y}\right) ${/tex}
06. Fie {tex}$c\in \mathbb{R}$ {/tex}. Atunci {tex}$ \displaystyle \log_a x^c=c\cdot log_a x${/tex}
07. {tex}$ \displaystyle \log_a x\cdot \log_x a=1${/tex}
08. {tex}$ \displaystyle \log_a x=\frac{\log_y x}{\log_y a}${/tex}
09. {tex}$ \displaystyle a>1 , x \in (0,1) \Rightarrow \log_a x < 0 ${/tex}
10. {tex}$ \displaystyle a>1 , x>1 \Rightarrow \log_a x > 0 ${/tex}
11. {tex}$ \displaystyle a \in (0,1) , x \in (0,1) \Rightarrow \log_a x > 0 ${/tex}
12. {tex}$ \displaystyle a \in (0,1) , x>1 \Rightarrow \log_a x < 0 ${/tex}
13. Dacă {tex}$ \displaystyle a>1${/tex} funcţia {tex}$ \displaystyle f_a:\mathbb{R}^{+}-\{0\}} \rightarrow \mathbb{R}^{+}-\{0\}}, f_a (x)=\log_a x${/tex} este strict crescătoare, adică pentru {tex}$ \displaystyle x>y${/tex}, avem {tex}$ \displaystyle \log_a x>\log_a y${/tex}
14. Dacă {tex}$ \displaystyle a \in (0,1) ${/tex} funcţia {tex}$ \displaystyle f_a:\mathbb{R}^{+}-\{0\}} \rightarrow \mathbb{R}^{+}-\{0\}}, f_a (x)=\log_a x${/tex} este strict descrescătoare, adică pentru {tex}$ \displaystyle x>y${/tex}, avem {tex}$ \displaystyle \log_a x<\log_a y${/tex}
15. Fie {tex}$ \displaystyle c\in\mathbb{R}-\{0\}$ {/tex}. Atunci {tex}$ \displaystyle \log_{a^c} x=\frac{1}{c} \log_a x${/tex}
16. Fie {tex}$ \displaystyle x\in\mathbb{R}, a>0, a\not=1${/tex}. Atunci {tex}$ \displaystyle a^x=e^{x \ln a}$ \displaystyle {/tex}.
Pentru fiecare dintre proprietăţile unde nu sunt puse condiţii pentru {tex}$ \displaystyle a, x, y ${/tex} , se subînţeleg condiţiile din definiţie.
