Partea stângă a inegalității se poate demonstra utilizând inegalitatea Cebâșev (cea pentru două șiruri monoton crescătoare), iar partea dreaptă, pe baza inegalităților triunghiului.
În continuare, vom privi membrul din mijloc (pe care îl notăm cu  ) ca fiind suma de produse:
) ca fiind suma de produse:  și considerăm, fără a restrânge generalitatea, că lungimile laturilor sunt în ordinea
și considerăm, fără a restrânge generalitatea, că lungimile laturilor sunt în ordinea 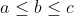 . Atunci avem, pe de o parte
. Atunci avem, pe de o parte 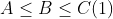 (unei laturi mai mari i se opune un unghi mai mare) și, pe de altă parte,
(unei laturi mai mari i se opune un unghi mai mare) și, pe de altă parte,  .
.
Demonstrație partea stângă:
Inegalitatea lui Cebâșev, aplicată mărimilor din (1) și (2), se va scrie:  .
.
Demonstrație partea dreaptă:
Cum  (inegalitatea triunghiului), rezultă
(inegalitatea triunghiului), rezultă  . Analog,
. Analog,  și
și  . Adunând membru cu membru relațiile (*), (**) și (***), obținem:
. Adunând membru cu membru relațiile (*), (**) și (***), obținem:  , care înseamnă
, care înseamnă 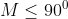 .
.